Formule de bază Combinatorice. Combinatorică: Formula de permutare, plasare

Permutarea este o combinație de elemente de la N. Elemente diferite luate într-o anumită ordine. În permutarea, procedura de urmat de elemente este importantă și totul trebuie să fie implicat în permutarea N. Elemente.

Sarcina: găsiți toate permutațiile posibile pentru secvența numerelor 1, 2, 3.
Există următoarele permutări:

1: 1 2 3
2: 1 3 2
3: 2 1 3
4: 2 3 1
5: 3 1 2
6: 3 2 1

Rearanjamente fără repetări

Numărul de permutări pentru N de diferite elemente este N!. Într-adevăr:

• În primul rând poate fi plasat oricare dintre ele N. Elemente (opțiuni totale N.),
• În a doua poziție poate fi plasată oricare dintre celelalte (N-1) Elemente (opțiuni totale N · (n-1)),
• dacă continuați această secvență pentru toți N. Locuri, vom obține: N · (N-1) · (n-2) · · 1, adică totul N! permutări.

Luați în considerare sarcina de a obține toate permutările numerelor 1 ... N. (adică secvențele de lungime N.), în cazul în care fiecare dintre numere este exact o dată. Există multe opțiuni pentru obținerea permutațiilor. Cu toate acestea, cel mai adesea a rezolvat sarcina de a genera permutări în lexicografică (vezi exemplul de mai sus). În acest caz, toate permutațiile sunt sortate mai întâi la început, apoi pe al doilea, etc. în ordine ascendentă. Astfel, primul va fi permutare 1 2 ... nȘi ultimul N n-1 ... 1.

Luați în considerare algoritmul de rezolvare a problemelor. Se administrează secvența inițială a numerelor. Pentru a obține fiecare permutare următoare, trebuie să efectuați următorii pași:

• Trebuie să vizualizați permutarea actuală din partea stângă dreaptă și, în același timp, asigurați-vă că fiecare element de permutare (element cu un număr mare) nu este mai mult decât cel precedent (element cu un număr mai mic). De îndată ce acest raport este afectat, este necesar să se oprească și să marcheze numărul curent (poziția 1).
• Din nou, pentru a vizualiza calea călătorită spre dreapta până când vom face înainte de prima zi, care este mai mare decât în \u200b\u200bpasul anterior.
• Schimbați două elemente obținute locuri.
• Acum, în partea matricei, care este plasată în partea dreaptă a poziției 1, trebuie să sortați toate numerele în ordine ascendentă. Dinainte de aceasta, au fost deja înregistrate în ordine descrescătoare. Este necesar să transformi pur și simplu această parte a subsecvenței.

Astfel, obținem o nouă secvență care va fi considerată cea inițială în pasul următor.

Vânzări pe C ++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

#Include.
utilizarea spațiului de nume STD;

{
int s \u003d a [i];
a [i] \u003d a [j];
a [j] \u003d s;
}
bOOL NEXTSET (INT * A, INT N)
{
int j \u003d n - 2;
În timp ce (j! \u003d -1 && a [j]\u003e \u003d a) j -;
dacă (J \u003d\u003d -1)
Întoarce-te fals; // nu mai nu mai
int k \u003d n - 1;
în timp ce (a [j]\u003e \u003d a [k]) k-;
swap (a, j, k);
int l \u003d j + 1, r \u003d n - 1;
În timp ce (L. Swap (A, L ++, R-);
Întoarce-te adevărat;
}
void Imprimare (Int * A, Int N) // Concluzie peretrestanovka.
{
Static int num \u003d 1; // Numărul de permutări
Cut.width (3);
Cout.<< num++ << ": " ;
pentru (int i \u003d 0; i< n; i++)
Cout.<< a[i] << " " ;
Cout.<< endl;
}
int principal ()
{
int n, * a;
Cout.<< "N = " ;
CIN \u003e\u003e;
a \u003d nou int [n];
pentru (int i \u003d 0; i< n; i++)
A [i] \u003d I + 1;
Imprimare (A, N);
În timp ce (Nextset (A, N))
Imprimare (A, N);
CIN.GET (); CIN.GET ();
retur 0;
}

Rezultatul executării

Rearanjamente cu repetare

O atenție specială merită sarcina de a genera permutări N. Elemente dacă elementele de secvență pot fi repetate. Să presupunem că secvența inițială este formată din elemente n 1, n 2 ... n kunde elementul n 1. Repetat r1. timp, n 2. Repetat r2. ori, etc. În care n 1 + n 2 + ... + n k \u003d n. Dacă luăm în considerare totul n 1 + n 2 + ... + n k Elemente de permutare cu repetiții sunt diferite, apoi toate opțiunile diferite pentru permutări ( n 1 + n 2 + ... + n k)! . Cu toate acestea, printre aceste permutări nu sunt toate diferite. De fapt, toate r1. Elemente n 1. Putem rearanja în locuri unul cu celălalt și nu se va schimba de la asta. În mod similar, putem rearanja elementele n 2., n 3. și așa mai departe. În cele din urmă avem r 1! Opțiuni de înregistrare pentru aceeași permutare cu diferite aranjamente de repetare a elementelor n 1.. Astfel, orice permutare poate fi înregistrată r 1! · R 2! · ... · R K! moduri. În consecință, numărul de rearanjamente diferite cu repetiții este

Pentru a genera rearanjamente cu repetiții, puteți utiliza algoritmul pentru generarea de permutări fără repetări mai sus. Introducem un element repetat într-o matrice A. Mai jos este codul programului pentru a genera rearanjamente cu repetări (numai codul principal () este modificat).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

#Include.
utilizarea spațiului de nume STD;
swap (Int * A, Int I, Int J)
{
int s \u003d a [i];
a [i] \u003d a [j];
a [j] \u003d s;
}
bOOL NEXTSET (INT * A, INT N)
{
int j \u003d n - 2;
În timp ce (j! \u003d -1 && a [j]\u003e \u003d a) j -;
dacă (J \u003d\u003d -1)
Întoarce-te fals; // nu mai nu mai
int k \u003d n - 1;
în timp ce (a [j]\u003e \u003d a [k]) k-;
swap (a, j, k);
int l \u003d j + 1, r \u003d n - 1; // asigurăm partea rămasă a secvenței
În timp ce (L. Swap (A, L ++, R-);
Întoarce-te adevărat;
}
void Imprimare (Int * A, Int N) // Concluzie peretrestanovka.
{
Static int num \u003d 1; // Numărul de permutări
Cut.width (3); // lățimea câmpului de ieșire Numărul de permutare
Cout.<< num++ << ": " ;
pentru (int i \u003d 0; i< n; i++)
Cout.<< a[i] << " " ;
Cout.<< endl;
}
int principal ()
{
int n, * a;
Cout.<< "N = " ;
CIN \u003e\u003e;
a \u003d nou int [n];
pentru (int i \u003d 0; i< n; i++)
A [i] \u003d I + 1;
A \u003d 1; // element repetat
Imprimare (A, N);
În timp ce (Nextset (A, N))
Imprimare (A, N);
CIN.GET (); CIN.GET ();
retur 0;
}

Rezultatul lucrării algoritmului de mai sus:

Pentru ca materialul, a fost mai ușor de navigat, adăugați conținutul acestui subiect:

Introducere Seturi și mostre.

În acest subiect, luați în considerare conceptele de bază ale combinatoricii: permutări, combinații și plasare. Noi aflăm esența și formulele pentru care le puteți găsi cantitatea lor.

Pentru a lucra, vom avea nevoie de informații auxiliare. Să începem cu un astfel de concept matematic fundamental ca mulți. În detaliu, conceptul de set a fost dezvăluit în subiectul "Conceptul unui set. Modalități de setare a seturilor".

Poveste foarte scurtă despre set: arată ascunde

Pe scurt: setul este numit un anumit set de obiecte. Seturi de înregistrare în paranteze curbate. Procedura de înregistrare a elementelor de rol nu se joacă; Elementele repetate nu sunt permise. De exemplu, un set de numere de 1111555999 va fi: $ \\ (1,5,9 \\) $. Multe scrisori consonante în cuvântul "tigru" este: $ \\ (t, r, r, n, k \\) $. Înregistrarea 5 $ \\ în A $ înseamnă că elementul 5 aparține SET $ a \u003d \\ (1,5,9 \\) $. Numărul elementelor din setul final se numește putere Acest set și denotă $ | a | $. De exemplu, pentru setul de $ a \u003d \\ (1.5.9 \\) $ care conține 3 elemente, avem: $ | A | \u003d $ 3.

Luați în considerare un anumit set finit non-goală de $ u $, puterea de a căruia este $ n $, $ | u | \u003d n $ (adică, există elemente de $ n $ într-un mai multe $ u $). Introducem un astfel de lucru ca probă (Unii autori se referă la tuple). Sub selectarea volumului de $ k $ de $ N $ elemente (abreviat $ (n, k) $ - eșantion), vom înțelege setul de elemente $ (A_1, A_2, \\ Ldots, A_K) $, unde $ A_I \\ în u $. Proba se numește comandată dacă este setată la ordinea elementelor. Două eșantioane comandate, care diferă numai de ordinea elementelor, sunt diferite. Dacă ordinea elementelor eșantionului nu este esențială, eșantionul este numit dezordonat.

Rețineți că în definirea eșantionului nu se spune nimic despre repetarea elementelor. Spre deosebire de seturi de seturi, elementele eșantionului pot fi repetate.

De exemplu, ia în considerare setul de $ u \u003d \\ (A, B, C, D, E \\) $. Set $ \u200b\u200bu $ conține 5 elemente, adică $ | U | \u003d $ 5. Eșantionul fără repetări poate fi ca acesta: $ (A, B, C) $. Această probă conține 3 elemente, adică Volumul acestei eșantioane este 3. Cu alte cuvinte, este $ (5.3) $ - eșantion.

Eșantionarea cu repetiții poate fi ca aceasta: $ (A, A, A, A, A, C, C, D) $. Acesta conține 8 elemente, adică 8. Este 8. Cu alte cuvinte, acesta este $ (5.8) $ - eșantion.

Luați în considerare încă două $ (5.3) $ - eșantion: $ (a, b, b) $ și $ (B, A, b) $. Dacă credem că mostrele noastre dezordonate, atunci eșantionul $ (A, B, B) $ este egal cu $ (B, A, B) $ eșantion, adică $ (a, b, b) \u003d (b, a, b) $. Dacă credem că eșantioanele comandate, apoi $ (A, B, B) \\ Neq (B, A, B) $.

Luați în considerare un alt exemplu, un pic mai puțin abstract :) Să presupunem, în coș există șase bomboane și toate acestea sunt diferite. Dacă prima bomboană pusă în conformitate cu figura 1, a doua bomboană - figura 2 și așa mai departe, apoi cu bomboanele din coș, este posibil să se compare un astfel de set: $ u \u003d \\ (1,2,3 , 4,5,6 \\) $. Imaginați-vă că suntem la întâmplare, alergați mâna în coș pentru a scoate trei bomboane. Trageți bomboanele este o probă. De când scoatem 3 bomboane din 6, primim (6.3) -Screen. Ordinea aranjării bomboanelor în palma palmei este complet nesemnificativă, astfel încât această probă este dezordonată. Ei bine, și din moment ce toate bomboanele sunt diferite, apoi eșantion fără repetări. Deci, în această situație, vorbim descreen neordonat (6.3) fără repetări.

Acum vin din cealaltă parte. Ne vom imagina că suntem în planta pentru producția de bomboane, iar în această fabrică există bomboane patru soiuri. Setul de $ u $ în această situație este: $ u \u003d \\ (1,2,3,4 \\) $ (fiecare cifră este responsabilă pentru varietatea de bomboane). Acum, imaginați-vă că toată bomboanele vor fi menționate într-o singură bilă, despre care stăm. Și, înlocuind palmele, din acest flux, selectăm 20 de bomboane. Bomboanele din piatră este o probă. Are rolul aranjamentului de bomboane în joc la îndemână? În mod natural, nu, astfel încât eșantionul nu este neetichetat. Doar 4 soiuri de bomboane și selectăm douăzeci de piese dintr-un flux total - repetarea soiurilor sunt inevitabile. În același timp, eșantioanele pot fi cele mai diferite: putem chiar să avem toate bomboanele unui soi. În consecință, în această situație avem de-a face cu dezordonate (4.20) -Marus cu repetări.

Luați în considerare câteva exemple mai multe. Lăsați diferitele 7 litere scrise în cuburi: K, O, N, F, E, T, A. Aceste litere formează un set de $ u \u003d \\ (k, o, n, f, e, t, a \\) $. Să presupunem din aceste cuburi dorim să facem un "cuvinte" de 5 litere. Scrisorile acestor cuvinte (de exemplu, "Konfe", "Tenko" și așa mai departe) Forma (7.5) -Seliți: $ (k, o, n, f, e) $, $ (t, e, n ,, O) $, etc. Evident, ordinea scrisorilor într-o astfel de eșantion este importantă. De exemplu, cuvintele "Nokft" și "Kfton" sunt diferite (deși constau din aceleași litere), pentru că nu coincid ordinea scrisorilor. Nu există repetări de scrisori în astfel de cuvinte, pentru că sunt disponibile doar șapte cuburi. Deci, setul de litere ale fiecărui cuvânt este un argument ordonat (7,5) fără repetări.

Un alt exemplu: facem tot felul de numere de opt cifre de patru cifre 1, 5, 7, 8. De exemplu, 11111111, 15518877, 88881111 și așa mai departe. Set $ \u200b\u200bu $ este: $ u \u003d \\ (1,5,7,8 \\) $. Numerele fiecărei componente (4.8) -Screen. Ordinea numerelor este printre înregistrarea, adică. Eșantion ordonat. Repetițiile sunt permise, deci aici avem de-a face cu un ordonat (4.8) -method cu repetări.

Plasarea fără repetări de $ N $ elemente pe $ k $

Plasarea fără repetări de $ N $ Elemente pe $ K $ - Comandat $ (N, K) $ - eșantion fără repetări.

Deoarece elementele nu pot fi repetate în eșantionul în considerare, atunci nu putem selecta mai multe elemente la eșantion decât în \u200b\u200bsetul inițial. În consecință, pentru astfel de eșantioane este adevărata inegalitate: $ n≥ k $. Numărul de destinații de plasare fără repetiții de $ N $ elemente pe $ k $ este determinat prin următoarea formulă:

\\ Începe (ecuație) a_ (n) ^ (k) \u003d \\ frac (n{(n-k)!} \end{equation} !}

Ce inseamna semnul?: arată ascunde

Înregistrarea "N!" (Citiți "en factorial") denotă produsul tuturor numerelor de la 1 la N, adică

$$ N! \u003d 1 \\ cdot2 \\ cdot 3 \\ cdot \\ ldots \\ cdot n $$

Prin definiție, se presupune că $ 0! \u003d 1! \u003d $ 1. De exemplu, găsiți 5!:

$ 5! \u003d 1 \\ CDOT 2 \\ CDOT 3 \\ CDOT 4 \\ CDOT 5 \u003d 120. $.

Exemplu №1.

Alfabetul constă dintr-o multitudine de simboluri $ E \u003d \\ (+, *, 0,1, F \\) $. Definim numărul de astfel de cuvinte triximaliste în acest alfabet care nu conțin litere repetate.

Sub cuvintele trixime, vom înțelege expresiile formularului "+ * 0" sau "0F1". Într-un set de $ cinci elemente, prin urmare, scrisorile de trei cuvinte vizate (5.3) - Clifts. Prima întrebare: Aceste eșantioane sunt comandate sau nu? Cuvintele care diferă numai prin ordinea scrisorilor se bazează în mod diferit, astfel încât ordinea elementelor din eșantion este importantă. Deci, eșantionul este comandat. A doua întrebare: Permiteți repetarea sau nu? Răspunsul la această întrebare dă condiție: cuvintele nu trebuie să conțină scrisori repetate. Rezumează: scrisorile fiecărui cuvânt care satisface starea problemei, formează o comandă comandată (5.3) fără repetări. Cu alte cuvinte, scrisorile fiecărui cuvânt de plasare fără repetări de 5 elemente de 3. Iată exemple de astfel de locuri:

$$ (+, *, F), \\ (*, +, f), \\; (1, +, 0) $$

Suntem, de asemenea, interesați de numărul total al acestor cazare. Conform formulei (1), numărul de destinații de plasare fără repetări de 5 elemente de 3 va fi:

$$ a_ (5) ^ (3) \u003d \\ frac (5{(5-3)!}=\frac{5!}{2!}=60. $$ !}

Acestea. Este posibil să se facă 60 de cuvinte trixime, literele ale căror litere nu vor fi repetate.

Răspuns: 60.

Plasarea cu repetiții de $ N $ elemente pentru $ k $

Plasarea cu repetiții de $ N $ Elemente pentru $ K $ - Comandat $ (N, K) $ - Eșantionare cu repetiții.

Numărul de repetiții de la $ n $ elemente pe $ k $ este determinat prin următoarea formulă:

\\ Începe (ecuație) \\ bara (a) _ (n) ^ (k) \u003d n ^ k \\ capătul (ecuație)

Exemplul nr. 2.

Câte numere de cinci cifre pot fi alcătuite din mai multe numere $ \\ (5,7.2 \\) $?

Din acest set, numerele pot fi alcătuite de numere de cinci cifre 55555, 75222 și așa mai departe. Numărul fiecărui astfel de formular numeric (3.5) -Screen: $ (5,5,5,5) $, $ (7,5,2,2,2) $. Să ne întrebăm: Ce este acest eșantion? În primul rând, numerele din numere pot fi repetate, așa că avem de-a face cu eșantioane cu repetiții. În al doilea rând, ordinea numărului de numere este printre cele importante. De exemplu, 27755 și 77255 - numere diferite. Prin urmare, avem de-a face cu variațiile comandate (3.5) cu repetări. Numărul total de astfel de eșantioane (adică numărul total de cinci cifre dorite) va fi găsită cu formula (2):

$$ \\ bar (a) _ (3) ^ (5) \u003d 3 ^ 5 \u003d 243. $.

În consecință, pot fi făcute 243 de cifre din numerele date.

Răspuns: 243.

Rearanjamente fără repetări de la $ n $ elemente

Rearanjament fără repetări de $ N $ elemente - comandate $ (n, n) $ - eșantion fără repetări.

De fapt, permutarea fără repetiții este un caz particular de plasare fără repetări atunci când volumul eșantionului este egal cu puterea setului de sursă. Numărul de permutări fără repetiții de la $ N $ elemente este determinat prin următoarea formulă:

\\ Începe (ecuație) p_ (n) \u003d n! \\ Capăt (ecuație)

Această formulă, apropo, este ușor de obținut, dacă considerăm că $ p_n \u003d a_ (n) ^ (n) $. Apoi primim:

$$ p_n \u003d a_ (n) ^ (n) \u003d \\ frac (n{(n-n)!}=\frac{n!}{0!}=\frac{n!}{1}=n! $$ !}

Exemplu numărul 3.

Congelatorul se află la cinci porții de înghețată din diferite firme. Câte moduri pot alege ordinea corecției lor?

Lăsați prima înghețată să corespundă figurii 1, cea de-a doua cifră 2 și așa mai departe. Obținem un set de $ u \u003d \\ (1,2,3,4,5 \\) $, care va reprezenta conținutul congelatorului. Procedura de taxă poate fi: $ (2,1,3,5) $ sau cam asa: $ (5,4,3,1,2) $. Fiecare set similar este (5.5) -Screen. Va fi comandat și fără repetiție. Cu alte cuvinte, fiecare astfel de eșantion este o permutare a 5 elemente ale setului original. Conform formulei (3), numărul total al acestor permutări este:

$$ p_5 \u003d 5! \u003d 120. $.

În consecință, există 120 de ordine de alegere a severității dovezilor.

Răspuns: 120.

Rearanjamente cu repetare

Rearanjare cu repetiții - comandate $ (n, k) $ - un eșantion cu repetiții în care elementul $ a_1 este repetat $ k_1 $ o dată, $ a_2 $ se repetă $ k_2 ori mai departe, la ultimul element $ A_R $, care este repetate $ k_r $ ori. În acest caz, $ k_1 + k_2 + \\ ldots + k_r \u003d k $.

Numărul total de rearanjații cu repetiție este determinat prin formula:

\\ Începe (ecuație) p_ (k) (k_1, k_2, \\ ldots, k_r) \u003d \\ frac (k{k_1!\cdot k_2!\cdot \ldots \cdot k_r!} \end{equation} !}

Exemplu numărul 4.

Cuvintele se bazează pe alfabetul de $ u \u003d \\ (A, B, D \\) $. Câte cuvinte diferite de la șapte caractere pot fi întocmite dacă litera "A" ar trebui repetată de 2 ori în aceste cuvinte; Scrisoarea "B" - 1 timp, și litera "D" - de 4 ori?

Iată exemple de cuvinte dorite: "AABDDDD", "Daddabd" și așa mai departe. Literele fiecărui cuvânt (3.7) - Corect cu repetiții: $ (A, A, B, D, D, D, D) $, $ (D, A, D, D, A, B, D) $ și etc. Fiecare astfel de eșantion constă din două elemente "A", un element "B" și patru elemente "D". Cu alte cuvinte, $ k_1 \u003d $ 2, $ k_2 \u003d 1 $, $ k_3 \u003d $ 4. Numărul total de repetări ale tuturor caracterelor, în mod natural, egale cu dimensiunea eșantionului, adică $ k \u003d k_1 + k_2 + k_3 \u003d 7 dolari. Înlocuirea acestor date în formula (4), vom avea:

$$ p_7 (2,1,4) \u003d \\ frac (7{2!\cdot 1!\cdot 4!}=105. $$ !}

În consecință, numărul total de cuvinte dorite este de 105.

Răspuns: 105.

Combinații fără repetări de la $ n $ elemente pe $ k $

Combinația fără repetări de $ n $ de elemente pe $ K $ este un $ (N, K) $ - un eșantion fără repetări.

Numărul total de combinații fără repetiții de $ N $ elemente pe $ k $ este determinat de formula:

\\ Începe (ecuație) c_ (n) ^ (k) \u003d \\ frac (n{(n-k)!\cdot k!} \end{equation} !}

Exemplu numărul 5.

Coșul conține carduri pe care numerele întregi sunt scrise de la 1 la 10. Din coș, 4 cărți scot și rezumă numerele scrise pe ele. Câte diferite seturi de carduri pot fi scoase din coș?

Deci, în această problemă, setul inițial este așa: $ u \u003d \\ (1,2,3,4,5,6,7,8,9,10 \\) $. Din acest set, alegem patru elemente (adică patru cărți din coș). Numerele elementelor extrase (10,4) -cake. Repetițiile nu sunt permise în acest eșantion, deoarece numerele tuturor cardurilor sunt diferite. Întrebarea este: Ordinea de alegere a cărților joacă un rol sau nu? Acestea., De exemplu, sunt eșantioanele de $ (1,2,7,10) $ și $ (10,2,7,7) $ sau nu sunt egale? Aici trebuie să vă referiți la starea problemei. Cardurile sunt eliminate pentru a găsi apoi cantitatea de elemente. Și acest lucru înseamnă că ordinea cardurilor nu este importantă, deoarece suma nu se va schimba de la schimbările locului condițiilor. De exemplu, un eșantion $ (1,2,7,10) $ și un eșantion $ (10,2,1,7,7) $ va corespunde aceluiași număr de $ 1 + 2 + 7 + 10 \u003d 10 + 2 + 1 + 7 \u003d 20 $. Concluzie: Din termenii sarcinii rezultă că avem de-a face cu eșantioane dezordonate. Acestea. Trebuie să găsim numărul total de secundari dezordonați (10,4) fără repetări. Cu alte cuvinte, trebuie să găsim numărul de combinații de 10 elemente ale software-ului 4. Utilizarea pentru această formulă (5):

$$ C_ (10) ^ (4) \u003d \\ frac (10{(10-4)!\cdot 4!}=\frac{10!}{6!\cdot 4!}=210. $$ !}

În consecință, numărul total de seturi dorite este de 210.

Răspuns: 210.

Combinații cu repetiții de $ N $ elemente pe $ k $

O combinație cu repetiții de $ N $ elemente pe $ k $ - $ - $ (N, K) $ - un eșantion cu repetiții.

Numărul total de combinații cu repetiții de $ N $ elemente pe $ k $ este determinată de formula:

\\ Începe (ecuație) \\ bara (c) _ (n) ^ (k) \u003d \\ frac ((n + k-1){(n-1)!\cdot k!} \end{equation} !}

Exemplul nr. 6.

Imaginați-vă că suntem la planta Cranhilor - chiar lângă transportor, care mișcă bomboanele patru soiuri. Lansați mâinile în acest flux și trageți douăzeci de bucăți. Câte diferite "combinații de bomboane" pot fi în mână?

Dacă presupunem că gradul întâi corespunde numărului 1, clasa a doua este numărul 2 și așa mai departe, apoi setul inițial în sarcina noastră este așa: $ U \u003d \\ (1,2,3,4 \\) $. Din acest set alegem 20 de elemente (adică, aceleași 20 de bomboane din transportor). Formulare de bomboane handiculoase (4.20) -Screen. Firește, va fi repetarea soiurilor. Întrebarea este că ordinea elementelor din eșantion joacă rolul sau nu? Din termenii sarcinii rezultă că ordinea rolului elementelor de rol nu se joacă. Nu avem nici o importanță dacă 15 lollipopuri vor fi localizate mai întâi, apoi 4 bomboane de ciocolată sau primele 4 bomboane de ciocolată și apoi 15 bomboane. Deci, avem de-a face cu o eșantionare neordonată (4.20) cu repetiții. Pentru a găsi numărul total de eșantioane, folosim formula (6):

$$ \\ bar (c) _ (4) ^ (20) \u003d \\ frac ((4 + 20-1){(4-1)!\cdot 20!}=\frac{23!}{3!\cdot 20!}=1771. $$ !}

În consecință, numărul total de combinații dorite este de 1771.

O sarcină . Determinați numărul de seturi comandate lungime r.care pot fi alcătuite din elemente ale setului X. (
) dacă selecția fiecărui element
, produse din toate seturile X..

Set comandat
- Acesta este un element decartan
constând din r.multiplicatori identici X.. Conform regulii, numărul de elemente ale setului
in aceeasi masura
. Am adus formula
.

Exemplu. Câte numere de telefon de patru cifre pot fi făcute dacă utilizați toate zece cifre?

Aici
, iar numărul de numere de telefon este egal

2.1.5. Plasarea fără repetări

O sarcină . Câte seturi comandate
pot fi alcătuite n.elemente de set X.Dacă toate elementele setului sunt diferite?

Primul element poți alege n.moduri. Dacă primul element este deja selectat, atunci al doilea element puteți alege numai
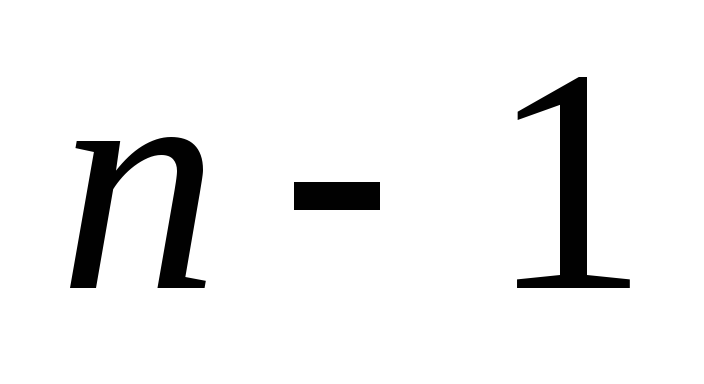moduri și dacă sunt deja selectate
element
, apoi element 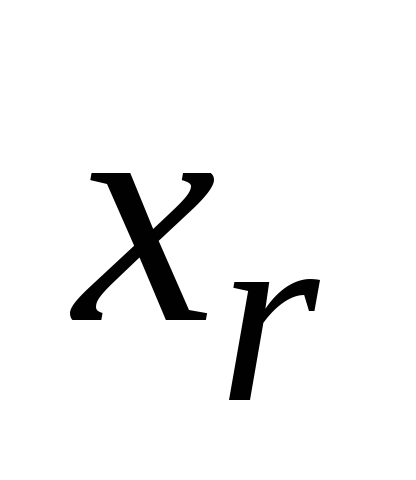poți alege
metode (repetarea elementului deja selectat nu este permisă). În conformitate cu regula, ajungem

Această formulă este scrisă diferit folosind denumirea.
. La fel de

.

Exemplu. Câte liste diferite ale câștigătorilor Jocurilor Olimpice (primul, al doilea, locul trei), dacă 20 au participat uman?

Aici
, este numărul dorit

2.1.6. Rearanjamente fără repetări

Luați în considerare un caz de plasare privat fără repetări: dacă
Apoi toate elementele stabilite sunt implicate în cazare X.. Probele au aceeași compoziție și diferă unul de celălalt numai prin ordinea elementelor. Astfel de eșantioane sunt numite permutări . Numărul de permutări este n.elementele sunt notate :

Exemplu.Câte moduri pot construi o coadă pe casier dacă șase persoane doresc să obțină un salariu?

2.1.7. Rearanjamente cu repetare

Lăsați multe X.cuprinde. k.elemente diferite:
.Permutarea repetiției compoziţie
vom numi un set de lungime ordonat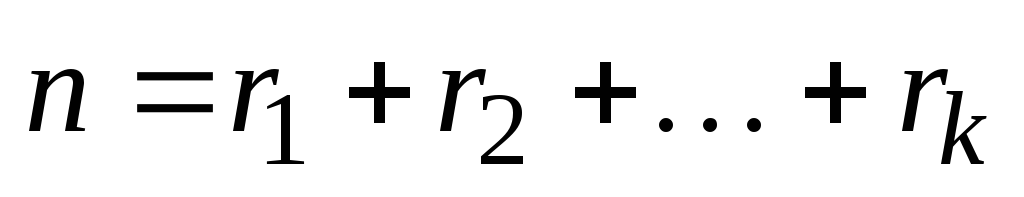
în care elementul Întâlni timp
. Numărul de astfel de permutări este indicat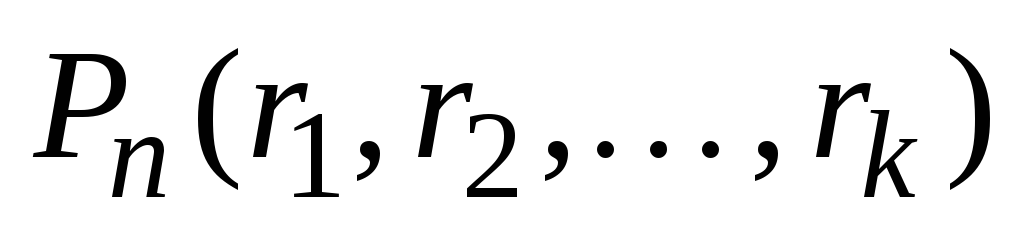
.

Exemplu. Din scrisori
scriem permutarea cu repetarea compoziției
. Lungimea ei
Și scrisoarea a.intră de 2 ori b.- de 2 ori, c.- o singura data. O astfel de permutare va fi, de exemplu,
sau
.

Derivăm formula pentru numărul de permutări cu repetiții. Intum toate aceleași elemente incluse în permutarea, diverși indici, adică. În loc de rearanjare
a primi
. Acum toate elementele de permutare sunt diferite, iar numărul acestor permutări este egal
. Primul element se găsește în eșantion timp. Vom elimina indicele la primul element (în exemplul nostru vom obține o permutare
), cu numărul de permutări diferite scade în o dată, pentru că La schimbarea ordinului acelorași elemente, eșantionul nostru nu se va schimba. Îndepărtați indicele din cel de-al doilea element - numărul de permutări va scădea timp. Și așa mai departe, la elementul cu numărul k.- numărul de permutări va scădea în timp. Avem o formulă

Exemplu. Câte "cuvinte" diferite pot fi obținute prin retransmiterea literelor cuvântului "transmisie"?

În acest cuvânt, litera "E" și "A" se găsește de două ori, restul o singură dată. Este vorba despre permutarea cu repetarea compoziției
lungime. Numărul acestor permutări este egal

2.1.8 Combinaţie

O sarcină . Câte seturi diferite de la r.elementele pot fi alcătuite dintr-un set care conține n.elemente?

Prim mai întâi compunem seturi comandate de r.elemente în fiecare. Numărul de astfel de seturi (acestea sunt plasate de la n.elemente in r.) Egal
. Acum luăm în considerare faptul că procedura de scriere a elementelor este indiferentă față de noi. În acest caz există o combinație de diverse de cazare care diferă numai pe ordinea elementelor. De exemplu, două destinații de plasare diferite
și
din cele două elemente corespund unei combinații
. Astfel, numărul de combinații în 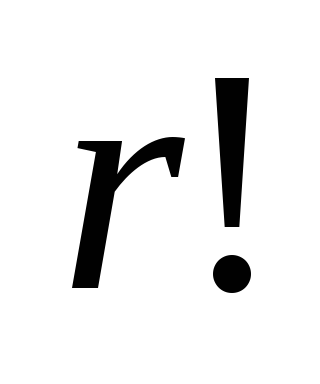ori mai puțin cazare :

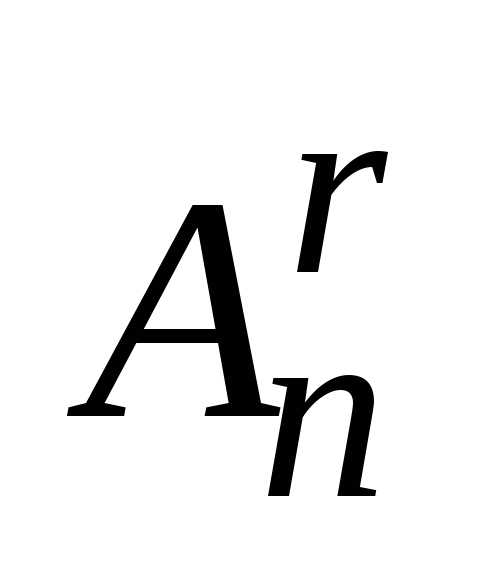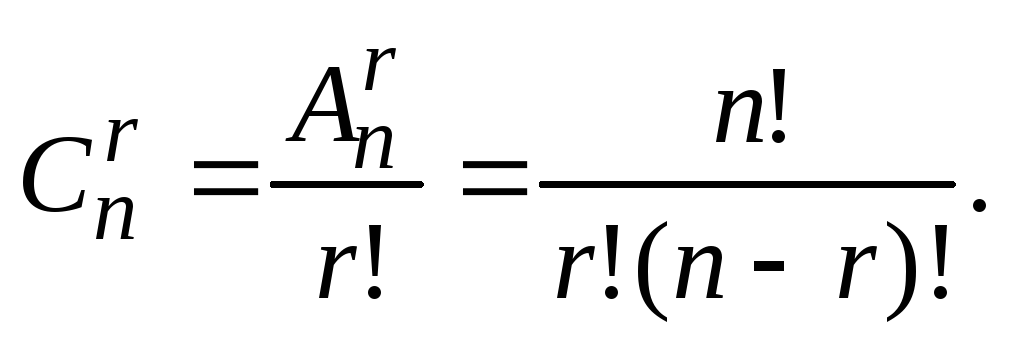
Exemplu. Numărul de moduri pe care le putem alege de la opt tipări trei

Numărul de cazare fără repetări n. de k. n. k. diverse coordonate.

Numărul de cazare fără repetiții este prin formula:

Exemplu: Câte moduri pot construi un număr de 3 cifre cu numere diferite care nu conțin numere 0?

Numărul de cifre
, dimensiunea vectorială cu diferite coordonate

Numărul de cazare de repetare

Numărul de cazare cu repetiții de la n. de k. - Acesta este numărul de moduri, câte pot n. diferite elemente pentru a construi vectori cu k. Coordonate, printre care pot fi aceleași.

Numărul de plasturi cu repetiții sunt prin formula:

.

Exemplu: Câte cuvinte de lungime 6 pot fi alcătuite din 26 de litere ale alfabetului latin?

Numărul de scrisori
, dimensiunea vectorului

Numărul de permutări fără repetări

Numărul de permutări fără repetări n. Elemente - acesta este numărul de moduri, câte pot fi plasate pe n diferite locuri n. diferite elemente.

Numărul de permutări fără repetiții este prin formula:

.

Cometariu: Puterea setului dorit DAR Este convenabil să căutați după formula:
Unde h. - numărul de moduri de a alege locurile potrivite; W. - numărul de moduri de a organiza elementele necesare asupra lor; z. - Numărul de moduri de a poziționa elementele rămase pe locurile rămase.

Exemplu. Câte moduri pot fi plasate pe un raft 5 cărți diferite? Câte cazuri sunt două cărți specifice A și B vor fi aproape?

În mod total de aranjare a 5 cărți pe 5 locuri - în mod egal = 5! = 120.

În sarcină h. - numărul de modalități de a alege două locuri în apropiere, h.= 4; W. - numărul de moduri de a aranja două cărți pe două locuri, w. = 2! = 2; z. - numărul de moduri de a organiza cele 3 cărți restul de 3 locuri, z.\u003d 3! \u003d 6. SO.
= 48.

Numărul de combinații fără repetări

Numărul de combinații fără repetări n. de k. - Acesta este numărul de moduri, câte pot n. Selectați diferite elemente k. bucăți fără a lua ordine.

Numărul de combinații fără repetiții este prin formula:

.

Proprietăți:

1)
; 2)
; 3)
;

4)
; 5)
; 6)
.

Exemplu. În urna 7 bile. Dintre acestea sunt 3 alburi. La ragii alegeți 3 bile. Câte moduri se poate face acest lucru? În câte cazuri vor fi exact un alb.

În mod total
. Pentru a obține numărul de moduri de a alege o minge albă (de 3 alb) și 2 bile negre (de la 4 negru), trebuie să multiplicați
și
Astfel, numărul dorit de moduri

Exerciții

1. Din cei 35 de studenți, clasa la sfârșitul anului a avut "5" în matematică - 14 persoane; în fizică - 15 persoane; în chimie - 18 persoane; în matematică și fizică - 7 persoane; în matematică și chimie - 9 persoane; în fizică și chimie - 6 persoane; Pentru toți cei trei subiecți - 4 persoane. Câți oameni au "5" la subiecții specificați? Câți oameni nu au "5" la subiecții specificați? Are doar "5" numai în matematică? Are doar "5" numai pe două subiecte?

2. Într-un grup de 30 de studenți, toată lumea știe cel puțin o limbă străină - engleză sau germană. Engleză Știu 22 Student, Germană - 17. Câți studenți știu ambele limbi? Câți studenți știu limba germană, dar nu știu engleza?

3. În 20 de camere ale pensiunii Institutului de Prietenie Populare live din Rusia; la 15 - din Africa; În 20 - din America de Sud. Și la 7 - ruși și africani trăiesc, în 8 - ruși și sud-americani; În 9 - africani și sud-americani; În 3 - și rușii și din America de Sud și Africanii. Elevii trăiesc în multe camere: 1) numai de pe un continent; 2) numai de la două continente; 3) numai africanii.

4. Fiecare dintre cei 500 de studenți este obligată să participe la cel puțin unul dintre cele trei cursuri speciale: în matematică, fizică și astronomie. Trei cursuri speciale vizitează 10 studenți, în matematică și fizică - 30 de studenți, în matematică și astronomie - 25; SpecCars numai în fizică - 80 de studenți. De asemenea, este cunoscut faptul că 345 de studenți sunt vizitați de matematică în matematică, în fizică - 145, pe astronomie - 100 de studenți. Câți studenți vizitează cursuri speciale pe astronomie? Câți studenți participă două cursuri speciale?

5. Bătrânul cursului a prezentat următorul raport privind educația fizică. Total - 45 de elevi. Secțiunea de fotbal - 25 de persoane, o secțiune de baschet - 30 de persoane, o secțiune de șah - 28 de persoane. În același timp, 16 persoane vizitează în același timp secțiunile de fotbal și de baschet, 18 - fotbal și șah, 17 - Baschet și șah, 15 persoane participă la toate cele trei secțiuni. Explicați de ce raportul nu a fost acceptat.

6. În acvariu 11 pește. Dintre acestea, 4 roșu, restul sunt aur. La cârpe alege 4 pește. Câte moduri se poate face acest lucru? Găsiți numărul de moduri de a face acest lucru, astfel încât între ei: 1) exact un roșu; 2) exact 2 aur; 3) cel puțin un roșu.

7. În lista 8 nume de familie. Dintre acestea, 4 sunt femei. În câte moduri pot fi împărțite în două grupuri egale, astfel încât fiecare are un nume de familie?

8. De la punte în 36 de cărți alegeți 4. Câte moduri de a face acest lucru, astfel încât: 1) toate hărțile erau diferite SIMED; 2) toate hărțile au fost un costum; 3) 2 roșu și 2 negru.

9. Scrisorile către, K, K, Y, Y, A, E, R. Câte moduri de a le plia într-un rând, astfel încât Kukakreu să fie dat.

10. Dases of the alfabetul tăiat cu litere, T, O, L, O, R, O, N, G, O, L, O, Oh, câte moduri de a le plia astfel încât cuvântul "otolyngolog" ar avea s-a întâmplat.

11. Dana curente carduri ABC cu litere L, și, T, E, P, A, T, Y, R, A. Câte moduri de a le plia într-un rând, astfel încât cuvântul "literatură" s-ar fi întâmplat.

12. 8 persoane sunt în linie. Câte moduri de a face acest lucru, astfel încât două persoane specifice A și B s-au găsit: 1) aproape; 2) la marginile coadajului;

13. 10 persoane stau jos pentru o masă rotundă timp de 10 locuri. În câte moduri se poate face astfel încât să existe: 1) două persoane specifice A și B; 2) trei persoane specifice A, B și S.

14. Din cele 10 numere arabe reprezintă un cod de 5 cifre. În câte moduri se poate face astfel încât: 1) toate cifrele erau diferite; 2) În ultimul loc, chiar cifra.

15. Din cele 26 de litere ale alfabetului latin (printre care 6 vocale), este compilat un cuvânt de șase litere. În câte moduri se poate face astfel încât în \u200b\u200bcuvântul: 1) exact o literă "A"; 2) exact o scrisoare de vocală; Exact două litere "A"; c) exact două vocale.

16. Câte numere de patru cifre sunt împărțite în 5?

17. Câte numere de patru cifre cu numere diferite sunt împărțite în 25?

19. Au fost aruncate trei oase de joc. Câte cazuri au scăzut: 1) exact 1 "șase"; 2) cel puțin un "șase".

20. Trei oase de joc aruncate. Câte cazuri vor fi: 1) toate diferite; 2) exact două numere identice.

21. Câte cuvinte cu litere diferite pot fi făcute din alfabetul A, B, C, D. Listează-le toate în ordine lexică: ABCD, ABCD ....

În primul rând, vom analiza conceptele de bază ale combinatoricii - eșantioane și tipurile lor: permutări, cazare și combinații. Este necesar să le cunoaștem pentru rezolvarea unei mari părți a EGE 2019 în matematică a ambelor niveluri, precum și de nouă clase pentru predarea OGE. Să începem cu exemplul.

Permutări. Numărarea numărului de permutări.

Imaginați-vă că ați ales o profesie, care aparent nu a fost legată de matematică, cum ar fi designerul interior. Imaginați-vă că clientul a exprimat o solicitare:

"Puneți 4 cărți pe raft, astfel încât volumele de burgundă și albastru să nu stau în apropiere. Arată-mi tot Opțiuni pentru aranjamente. Eu aleg cel mai preferat. "

Ce vei face? Cel mai probabil, veți începe să aranjați și să arătați. Cu toate acestea, pentru a nu fi confuz, să nu ratați niciuna dintre opțiunile posibile și să nu repetați, trebuie să o faceți pe un anumit sistem.

De exemplu, în primul rând, lăsăm volumul de burgundă în primul rând, poate exista verde sau portocaliu lângă el. Dacă există un volum verde pe locul al doilea, atunci poate fi portocaliu și albastru sau albastru și portocaliu. Dacă există un volum portocaliu în al doilea rând, atunci poate fi verde și albastru sau albastru și verde. Sunt obținute 4 opțiuni posibile.

În primul rând poate fi oricare dintre cele 4 volume, ceea ce înseamnă că procedura descrisă trebuie repetată de 3 ori. Cazul în care volumul albastru este în primul rând, se dovedește a fi același raționament.

Iar următoarele două cazuri diferă în ceea ce privește celelalte trei locuri ar trebui să existe volume de burgundă și albastru, dar nu aproape. De exemplu, când primul loc este în valoare de volumul verde, volumul portocaliu trebuie să stea pe locul trei pentru a separa volumele de burgundă și albastru care pot ocupa, respectiv sau locul al doilea și al patrulea sau al patrulea și al doilea.

Ca rezultat, am avut doar 12 opțiuni pentru aranjarea celei de-a patra cărți de pe raft cu o restricție dată. Există o mulțime sau puțin? Dacă petreceți un minut pentru a muta cărți și discuția despre opțiunea rezultată cu clientul, atunci, poate, este normal. 12 minute puteți purta cărți și vorbiți. (Încercați să calculați cât de mult ar avea permutările de permutările celei de-a patra cărți fără restricții?)

Acum, imaginați-vă că clientul are mai multe cărți decât 4, cel puțin 5. Este clar că opțiunile pentru aranjament vor fi mai mult și într-adevăr să le rearanjeze de la locul unde se află mai mult și să se confunde și să înceapă să repete mai ușor .. . Deci, graba în lupta fără pregătire nu mai merită. Trebuie să programați mai întâi opțiunile pe hârtie. Pentru concurs, vom purta volumele noastre de culoare și vom rearanja numerele pe hârtie. Pentru a face mai puțin greșită, mai întâi vom scrie toate opțiunile pentru permutare și apoi vom trece pe cei care se află sub restricție. Asa de:

"Aranjați 5 cărți pe raft, astfel încât volumele 1 și 2 să nu se apropie. Arată tot Opțiuni pentru permutări. "

Avem 5 cărți (sau 5 cifre), fiecare dintre acestea putând sta în primul rând. Vom face comprimatul pentru fiecare dintre aceste 5 cazuri. În al doilea rând, poate fi oricare dintre celelalte 4 cifre, pentru fiecare dintre ele, ne rezervăm coloana din placă.

În fiecare coloană, punem o pereche de linii în care unul dintre celelalte ore de 3 cifre este în picioare pe locul trei, iar cele două numere recente schimbă locurile. Așa că scriem cu atenție tot Opțiuni pentru permutare. Calculați numărul total.

5 (Mese) × 4.(coloană) × 3.(perechi de corzi) × 2.(linii) × 1 (opțiune) \u003d. 120 (Opțiuni).

Și în cele din urmă, scoateți din toate tabelele de opțiuni care conțin "12" sau "21". Acestea au fost 6 în primele și cele două semne și 12 în restul 3, doar 48 de opțiuni care nu îndeplinesc restricția. Deci, clientul trebuie să arate 120 - 48 \u003d 72 opțiuni pentru locația a 5 cărți. Va dura mai mult de o oră, chiar dacă petrecem într-o discuție despre fiecare opțiune doar un minut.

Numai unde ați văzut o persoană care va angaja un designer pentru a rearanja cinci cărți? Într-adevăr, astfel de sarcini apar în bibliotecile în care aveți nevoie pentru a plasa cărțile pentru confortul vizitatorilor, în librării mari, unde trebuie să plasați cărțile pentru a asigura o creștere a cererii etc. Asta este, în cazul în care cărțile nu sunt unități și nici măcar zeci, ci sute și mii.

Opțiunile de apel Permutațiile nu sunt numai pentru cărți. Acest lucru poate fi necesar pentru un număr mare de obiecte în aproape orice domeniu de activitate. Aceasta înseamnă că atât designerii, cât și oamenii din alte profesii pot avea nevoie de un instrument asistent și chiar mai bun pentru a facilita etapa pregătitoare, analiza rezultatelor posibile și reducerea volumului muncii neproductive. Astfel de instrumente au creat și creează oameni de știință matematici și apoi le dau societății sub formă de formule gata făcute. Matematica nu și-a ocuit atenția legată de permutări, precum și cu cazare și combinații de diferite elemente. Formulele corespunzătoare nu mai sunt un secol. Aceste formule sunt foarte simple, partea mai mică a societății "este acordată" în lecțiile de matematică școlară. Prin urmare, tot ceea ce a fost scris mai sus este o invenție în mod substanțial "o bicicletă", la care trebuia să recurg din cauza presupunerii că designerul de interior nu ar avea nevoie niciodată de matematică. Ei bine, renunțați la această presupunere. Repetăm \u200b\u200bconceptele matematice și apoi înapoi la sarcina raftului.

Combinatoriu. Regiunea matematică este chemată, în care sunt studiate întrebări cu privire la numărul de combinații diferite subordonate acestor sau nu pot fi alcătuite din elemente ale unui set dat. Prin constituirea unei combinații, de fapt, selectăm diferite elemente din acest set și le combinăm în grupuri în funcție de nevoile noastre, astfel încât în \u200b\u200bloc de cuvântul "combinații", cuvântul "eșantion" al elementelor adesea folosesc.

Formula pentru numărul de permutări.

Permutări Aceste probe de elemente sunt numite, care diferă numai prin ordinea elementelor, dar nu de elementele în sine.

Dacă sunt făcute permutările pe un set de n. Elemente numărul lor Determinată de formula
P n. = n.·( n.-1) · ( n.-2) ... 3 · 2 · 1 \u003d n.!

n.! - desemnarea care este utilizată pentru o scurtă înregistrare a activității tuturor numerelor naturale de la 1 la n. inclusiv și numită " n.-Factor "(tradus din" factor "" - multiplicator ").

Astfel, numărul total de permutări de 5 cărți P 5. \u003d 5! \u003d 1 · 2 · 3 · 4 · 5 \u003d 120, ceea ce avem mai sus. De fapt, am derivat această formulă pentru un exemplu mic. Acum voi rezolva mai mult exemplu.

Sarcina 1..

30 de volume sunt plasate pe raft. În câte moduri pot fi plasate astfel încât, în același timp, volumele 1 și 2 nu au stat în apropiere?

Decizie.

Definim numărul total de permutări de 30 de elemente cu formula P 30.=30!
Pentru a calcula numărul de permutări "inutile", definim mai întâi câte opțiuni în care volumul 2 este situat lângă primul din dreapta. În astfel de permutări, volumul 1 poate ocupa locurile de la primul la 29 și al doilea de la al doilea la 30 de ani - doar 29 de locuri pentru această pereche de cărți. Și cu fiecare poziție a primelor două volume, restul de 28 de cărți pot ocupa celelalte 28 locuri în orice ordine. Opțiuni pentru permutarea a 28 de cărți P 28.\u003d 28! În totalul opțiunilor "inutile" la locul celui de-al doilea volum la dreapta se va întoarce 29 · 28! \u003d 29!.
În mod similar, luați în considerare cazul în care volumul 2 este situat lângă 1, dar spre stânga. Se pare că același număr de opțiuni 29 · 28! \u003d 29!.
Deci, toate permutațiile "inutile" 2 · 29!, Și metodele necesare de aranjare a 30! -2 · 29! Calculați această valoare.
treizeci! \u003d 29! · 30; 30! -2 · 29! \u003d 29! · (30-2) \u003d 29! · 28.
Deci, trebuie să multiplicăm toate numerele naturale de la 1 la 29 și înmulțite cu 28 din nou.
Răspuns: 2.4757335 · 10 32.

Acesta este un număr foarte mare (după două alte 32 de cifre). Chiar dacă petreceți o secundă pentru fiecare permutare, veți avea nevoie de miliarde de ani. Merită să se realizeze o astfel de cerință a clientului sau este mai bine să se poată susține în mod rezonabil și să insiste asupra aplicării restricțiilor suplimentare?

Rearanjamente și probabilitate Teoria.

Mai des, necesitatea de a număra numărul de opțiuni apare în teoria probabilității. Continuați tema cărții următoare sarcină.

Sarcina 2..

Pe rafturile au fost 30 de volume. Copilul a scăzut cărți de pe raft și apoi le-a pus în ordine aleatorie. Care este probabilitatea ca el nu Puneți primul și al doilea lângă?

Decizie.

În primul rând, definim probabilitatea evenimentului A, care este faptul că copilul a pus primul și al doilea volum în apropiere.
Eveniment elementar - o anumită plasare a cărților pe raft. Este clar că numărul total toate Evenimentele elementare vor fi egale cu numărul total de permutări posibile P 30.=30!.
Numărul de evenimente elementare care conduc la evenimente A este egal cu numărul de permutări în care sunt în apropiere cele 1 și 2 și volume. Am considerat astfel de permutări, rezolvând sarcina anterioară și primim 2 · 29! permutări.
Probabilitatea determină împărțirea numărului de evenimente elementare favorabile prin numărul tuturor evenimentelor elementare posibile:
P (a) \u003d 2 · 29! / 30! \u003d 2 · 29! / (29! · 30) \u003d 2/30 \u003d 1/15.
Eveniment în - copil nu Puneți în apropierea volumului 1 și al doilea - opusul evenimentului A, ceea ce înseamnă probabilitatea sa P (b) \u003d 1 - P (a) \u003d 1-1 / 15 \u003d 14/15 \u003d 0,9333
Răspuns:0,9333.

Observație: Dacă nu este clar modul în care fracțiunile cu factoria sunt reduse, amintiți-vă că factorialul este o scurtă înregistrare a lucrării. Acesta poate fi întotdeauna vopsit în multiplicatori repetați pe nume și stres în numitor și în denominator.

Răspunsul a dovedit numărul apropiat de unul, înseamnă că, cu un astfel de cărți, au pus în mod aleatoriu două volume specificate de lângă mai dificil decât să nu se livreze.

Cazare. Numărarea numărului de cazare.

Presupun că clientul are multe cărți și este imposibil să le așezi pe toate pe rafturile deschise. Cererea sa este că trebuie să alegeți o anumită sumă de cărți și să le plasați frumos. Sa dovedit frumos sau urât, aceasta este întrebarea gustului clientului, adică. Vrea să vadă din nou tot Opțiuni și să luăm o decizie. Sarcina noastră este de a calcula numărul tuturor opțiunilor de cazare posibile pentru cărți, convinge în mod rezonabil și introduceți limitări rezonabile.

Pentru a rezolva situația, să presupunem mai întâi că "o mulțime" este de 5 cărți pe care avem doar un regiment și că numai 3 volume sunt montate pe ea. Ce facem?
Alegem una dintre cele 5 cărți și punem pe primul loc pe raft. Putem face acest lucru în a 5-a cale. Acum există două locuri pe raft și avem 4 cărți rămase. Putem alege cea de-a doua carte 4 moduri și am pus lângă unul dintre cele 5 mai întâi posibil. Astfel de perechi pot fi de 5,4. Există 3 cărți și un loc. O carte de la al treilea poate fi aleasă de 3 moduri și se pune lângă unul dintre cele 5 · 4 perechi posibile. Se pare 5 · 4 · 3 triple diverse. Aceasta înseamnă că modalitățile de a plasa 3 cărți de la 5 5 · 4 · 3 \u003d 60.

Figura arată doar 4 opțiuni pentru cazare din 60 posibil. Comparați imaginile. Rețineți că plasarea poate diferi de unul pe celălalt sau numai de ordinea elementelor, ca primele două grupuri sau compoziția elementelor, așa cum urmează.

Formula pentru numărul de cazare.

Cazare de n. Elemente in m. (locuri) se numesc astfel de eșantioane care au m. Elemente selectate din numărul de date n. Elementele diferă una de cealaltă sau compoziție de elemente sau prin ordinul locației lor.

Numărul de cazare afară n. de m. denotă. A. N m. și determinată de formula
A. N m \u003d. n.·( n. - 1) · ( n. - 2) · · ( n. − m. + 1) = n.!/(N-m)!

Să încercăm să calculăm pentru această formulă ANN.. Numărul de cazare afară n. de n..
ANN. = n.·( n.-unu)·( n.-2) · · ( n.-n. + 1) = n.·( n.-unu)·( n.-2) · ... · 1 \u003d n.!
În acest fel, ANN. = P n. = n.!

Nimic surprinzător este că numărul de cazare de la n. de n. Sa dovedit a fi egală cu numărul de permutări n. Elemente, deoarece am folosit toate set de elemente pentru a pregăti toate seturile, ceea ce înseamnă că nu mai pot diferi unul de celălalt cu compoziția elementelor, numai prin ordinul locației lor, și aceasta este permutarea.

Sarcina 3..

Câte moduri pot aranja 15 volume pe raft, dacă le alegeți din cele 30 de cărți disponibile?

Decizie.

Definim numărul total de cazare din 30 de elemente de 15 prin formula
A 30 15. \u003d 30 · 29 · 28 · ... (30-15 + 1) \u003d 30 · 29 · 28 · ... · 16 \u003d 202843204931727360000.
Răspuns: 202843204931727360000.

Veți posta cărți reale? Noroc! Luați în considerare cât de multe vieți vor trebui să treacă prin toate opțiunile.

Sarcina 4..

Câte moduri puteți aranja 30 de cărți pe două rafturi, dacă numai 15 volume sunt plasate pe fiecare dintre ele?

Decizie.

Metoda I.
Imaginați-vă că primul raft pe care îl umplem în același mod ca și în sarcina anterioară. Apoi vor fi opțiunile de plasare de la 30 de cărți A 30 15. \u003d 30 · 28 · 28 · ... · (30-15 + 1) \u003d 30 · 29 · 28 · ... · 16.
Și cu fiecare plasare a cărților pe primul raft, încă mai suntem P 15. \u003d 15! În metode putem aranja cărți pe cel de-al doilea raft. La urma urmei, pentru cel de-al doilea raft, am lăsat 15 cărți cu 15 locuri, adică. Sunt posibile numai permutările.
Toate căile vor fi A 30 15 · P 15În timp ce produsul tuturor numerelor de la 30 la 16 va fi înmulțit cu produsul tuturor numerelor de la 1 la 15, produsul tuturor numerelor naturale de la 1 la 30, adică treizeci!
Metoda II.
Acum, imaginați-vă că am avut un regiment lung în 30 de locuri. Am pus toate cele 30 de cărți pe el și apoi am văzut raftul în două părți egale pentru a satisface starea sarcinii. Câte opțiuni pentru aranjament ar putea fi? La fel de mult cum puteți face permutări de 30 de cărți, adică. P 30. = 30!
Răspuns: 30!.

Nu contează cum decideți sarcina matematică. Ați decizi ca să vă imaginați acțiunile în situația vieții. Este important să nu vă retrageți din logică în raționamentul dvs., astfel încât, în orice caz, veți obține răspunsul potrivit.

Plasarea și teoria probabilității.

În teoria probabilității, sarcina de plasare este oarecum mai puțin comună decât sarcinile altor tipuri de eșantioane, deoarece plasarea are mai multe caracteristici de identificare - atât ordinea cât și compoziția elementelor, ceea ce înseamnă mai puțin sunt supuse alegerii aleatorie.

Sarcina 5..

Pe rafturi există o colecție de scrieri ale unui autor în 6 volume. Cărțile din același format sunt arbitrare. Cititorul, fără a căuta, ia 3 cărți. Care este probabilitatea că a luat primele trei volume?

Decizie.

Eveniment A - cititor primele trei volume. În ceea ce privește ordinea de alegere, el le-ar putea lua în a 6-a cale. (Aceasta este permutările din cele 3 elemente. P 3. \u003d 3! \u003d 1 · 2 · 3 \u003d 6, care este ușor de listat 123, 132, 213, 231, 312, 321.)
Astfel, numărul evenimentelor elementare favorabile este egal cu 6.
Numărul total de evenimente elementare posibile este egal cu numărul de cazare de la 6 la 3, adică A. 6 3 \u003d 6 · ... · (6-3 + 1) \u003d 6,5 · 4 \u003d 120.
P (a) \u003d 6/120 \u003d 1/20 \u003d 0,05.
Răspuns: 0,05.

Combinaţie. Numărarea numărului de combinații.

Iar ultimul caz este toate cărțile clientului de aceeași culoare și o dimensiune, dar numai unele dintre ele sunt plasate pe raft. Se pare că designerul nu ar avea nici o problemă, să aleagă atât de multe cărți din numărul total, după cum aveți nevoie și să le plasați pe raft într-o ordine arbitrară, deoarece cărțile sunt indistinguizate în exterior. Dar ele diferă și semnificativ! Aceste cărți sunt diferite în conținut. Și clientul nu poate fi cu toții unde se află tragediile lui Shakespeare și unde detectivii din Rex Stama, pe raftul deschis sau în dulap. Astfel, avem o situație în care compoziția elementelor eșantionului este importantă, dar ordinea locației lor este nesemnificativă.

Figura prezintă două eșantioane din "Colecția de scrieri ale unui autor în 5 volume". Primul vă va plăcea clientului mai mult, dacă recide adesea lucrările timpurii ale acestui autor, plasate în primele trei volume, al doilea - dacă se adresează mai des la lucrările târzii plasate în ultimele volume. Ne uităm la ambele grupuri la fel de frumoase (sau la fel de urât) și nu contează dacă grupul va fi localizat ca 123 sau 321 ...

Formula pentru numărul de combinații.

Probele neordonate sunt numite de n. Elemente in m. Și indicați DIN N m..
Numărul de combinații Determinată de formula DIN N m \u003d. n!/(n. - m)! / m!

În această formulă, există doi divizori și un simbol este folosit ca semn de divizare. / ", care este mai convenabil pentru pagina web. Dar diviziunea poate fi, de asemenea, denotată de un colon" : "Sau o linie orizontală" --- ". În ultimul caz, formula arată ca o fracție obișnuită în care divizia secvențială este reprezentată de doi factori din numitor. . Pentru cei care sunt mai ușor de înțeles sub formă de fracțiuni, toate formulele sunt duplicate la început și la sfârșitul paginii. Vizualizarea soluțiilor la sarcini Comparați intrarea mea cu obișnuit pentru dvs.
În plus, toți multiplicatori și divizoare în această formulă sunt lucrări de numere naturale succesive, astfel încât fracțiunea este bine redusă dacă este scrisă în detaliu în detaliu. Dar mi-e dor de o abreviere detaliată în sarcini, este ușor să-l verificați singur.

Este clar că pentru aceleași seturi de sursă de la n. elemente și volume identice de probă (prin m. Elemente) Numărul de combinații ar trebui să fie mai mic decât numărul de cazare. La urma urmei, atunci când numărați cazare pentru fiecare grup selectat, încă luăm în considerare toate permutațiile celor selectați m. Elemente și la calcularea combinațiilor, nu luați în considerare: Cu n m. = A n M./P M. = n!/(n-m.)!/m!

Sarcina 6..

Câte metode pot fi aranjate 15 volume pe raft, dacă le alegeți din cele 30 de cărți nedeterminate de indistructurabile?

Decizie.

Rezolvăm această sarcină în contextul designului designerului de interior, deci ordinea următoarelor cărți pe raftul celor 15 cărți identice selectate nu contează. Este necesar să se determine numărul total de combinații de 30 de elemente de 15 prin formula
DIN 30 15 = 30! /(30 − 15)!/15! = 155117520.
Răspuns: 155117520.

Sarcina 7..

Câte moduri puteți aranja 30 de cărți de indistructura externă pe două rafturi, dacă doar 15 volume sunt plasate pe fiecare dintre ele?

Dacă răspundem la această întrebare din punctul de vedere al designerului interior, atunci ordinea cărților pe fiecare raft este nesemnificativă. Dar clientul poate fi important sau indiferent de modul în care sunt distribuite cărțile printre rafturi.
1) De exemplu, dacă ambele rafturi sunt aproape, ambele sunt deschise, atât la aceeași altitudine, atunci clientul poate spune că nu contează. Apoi, răspunsul este evident - 1 mod, deoarece atunci când este amenajat, sunt utilizate toate cele 30 de cărți și nu sunt luate în considerare permutări.
2) Dar când unul dintre rafturi este prea mare, clientul este important pe care sunt localizate cărți despre el. În acest caz, răspunsul va fi același ca în problema anterioară - metodele de 15511.7520, deoarece primul raft este completat de mostre - combinații de 30 până la 15 și pe al doilea loc rămas de 15 cărți, cu excepția permutațiilor.

Deci, există astfel de sarcini de formulare că răspunsurile pot fi obținute ambigue. Pentru o soluție exactă, sunt necesare informații suplimentare pe care de obicei le obținem din contextul situației. Creatorii sarcinilor de examinare, de regulă, nu permit o dublă interpretare a stării problemei, formulați este oarecum mai lungă. Cu toate acestea, dacă aveți îndoieli, este mai bine să se aplice profesorului.

Combinație și teoria probabilității.

În teoria probabilității, sarcina de combinații se găsește cel mai adesea, deoarece gruparea fără ordinea de interes este mai importantă pentru elementele indistructurabile. Dacă unele elemente diferă semnificativ între ele, sunt dificil de ales accidental, există linii directoare pentru selecția non-aleatorie.

Sarcina 8..

Pe rafturi există o colecție de scrieri ale unui autor în 6 volume. Cărțile sunt la fel de decorate și arbitrare. Cititorul ia la 3 cărți aleatorii. Care este probabilitatea că a luat primele trei volume?

Decizie.

Eveniment A - cititor primele trei volume. Acesta este primul volum 1, al doilea și al treilea. Excluderea ordinii în care a ales cărți, dar numai prin rezultatul final, el le-ar putea lua într-un fel. Numărul evenimentelor elementare favorizate - 1.
Numărul total de evenimente elementare posibile este egal cu numărul de grupuri de 6 până la 3 formate fără a lua în considerare procedura de urmat de elementele din grup, adică egală cu numărul de combinații De la 6 3. \u003d 6! / 3! / (6 - 3)! \u003d 4 · 5 · 6 / (1 · 2 · 3) \u003d 4 · 5 \u003d 20.
P (a) \u003d 1/20 \u003d 0,05.
Răspuns: 0,05.

Comparați această sarcină cu sarcina 5 (pentru plasare). În ambele sarcini, condiții foarte asemănătoare și exact aceleași răspunsuri. În esență, este doar aceeași situație a gospodăriei și, în consecință, aceeași sarcină care poate fi interpretată într-un fel sau altul. Principalul lucru este că atunci când se calculează evenimentele elementare, atât favorabile, cât și tuturor posibil, a existat o singură înțelegere a situației.

Comentarii finale.

Pentru o ieșire strictă a tuturor formulelor (pe care nu le-am dat aici) utilizate două reguli de bază ale combinatoricii:

Regula de multiplicare (regula " și"). Potrivit lui, dacă un element A poate fi selectat n. moduri și cu orice alegere un element B poate fi ales m. căi, apoi un cuplu a și B Puteți alege n · M. moduri.

Această regulă este generalizată pe o lungime arbitrară a secvenței.

Regula de finalizare (regula " sau"). Aceasta susține că dacă un element A poate fi selectat n. căile și elementul B pot fi alese m. căi, apoi alegeți a sau B este n + M. moduri.

Aceste reguli sunt necesare pentru a rezolva problemele.

Concept factorial Se aplică, de asemenea, la zero: 0! = 1 Deci, se crede că setul gol poate fi comandat numai de singura modalitate.

Calculați fabricile de numere mari prin multiplicarea directă pe calculator pentru o perioadă foarte lungă de timp, iar numerele foarte mari - și pe computer nu sunt rapide. Dar cum ați făcut acest lucru cu acest lucru înainte de crearea de computere și calculatoare? Chiar și la începutul secolului al XVIII-lea, J. Stirling și independent de el, A. Maurra a primit o formulă pentru un calcul aproximativ al factoriale, care este mai precis decât cel mai mult n.. Acum această formulă este numită formula Stirling:

Sarcina finală.

La rezolvarea problemelor pe teoria probabilității utilizând metode combinatoriale, este necesar să analizăm cu atenție situația propusă pentru a selecta corect tipul de eșantionare. Încercați să faceți acest lucru pe exemplul următoarei sarcini. Rezolvați-l, comparați răspunsul, apoi faceți clic pe buton pentru a deschide soluția mea.

Sarcina 9..

Din acvariu, în care 6 Sadans și 4 crap, un sacc de 5 pește prins. Care este probabilitatea ca exista 2 Szan si 3 crap printre ei?

Decizie.

Eveniment elementar - "într-un grup saccin de 5 pești". Evenimentul A - "Printre cele 5 pești prins sa dovedit a fi 3 crap și 2 Sazan. "
Lasa n. - Numărul total de evenimente elementare posibile, este egal cu numărul de moduri de grup de 5 pești. Pește total în acvariu 6 + 4 \u003d 10. În procesul de prindere a sacului de pește neexploahizat. (Nu știm dacă am prins peștele numit Bachka sau cu numele lui Koska. Mai mult decât atât, până când am scos sacul în sus și nu am privit-o, nici măcar nu îl cunoștem pe Sazan sau crap.) Astfel " Captură 5 pește de la 10 "înseamnă a face un tip de combinație de la 10 la 5.
n. = De la 10 5. = 10!/5!/(10 - 5)!
Tragerea cucului și privirea în ea, putem determina rezultatul favorabil sau nu, adică. Este captura de două grupe - 2 Szan și 3 crap?
Grupul Sazanov ar putea forma o alegere de 6 Sazanov la 2. și oricum, care dintre ei au urcat mai întâi în bord și care este al doilea, așa mai departe. Acesta este un tip de exemplu de combinație de 6 până la 2. Denotă de numărul total de astfel de eșantioane. m 1. Și o calculam.
m 1. = De la 6 2. = 6!/2!/(6 - 2)!
În mod similar, numărul total de grupe posibile de 3 crap este determinat de numărul de combinații de 4 până la 3. Denotați-l m 2..
m 2. = Cu 4 3. = 4!/3!/(4 - 3)!
Grupurile de crapuri și Sadans se formează într-un saccus independent unul de celălalt, astfel încât să calculeze numărul de evenimente elementare care să conducă la evenimentul A, folosim regula de combinatorie de multiplicare ("și" -Evilo). Deci, numărul total de evenimente elementare favorabile
m \u003d m 1 · m 2 = De la 6 2.· Cu 4 3.
Probabilitatea evenimentelor A determină cu formula P (a) \u003d m / n \u003d C6 2 · C 4 3 / C 10 5
Înlocuim toate valorile din această formulă, semnul factorials, reduceți fracțiunea și obțineți răspunsul:
P (a) \u003d 6! · 4! · (10-5)! / 2! / (6 - 2)! / 3! / (4 - 3)! / 10! \u003d 5/21 ≈ 0,238

Comentarii.
1) Combinațiile se găsesc de obicei în sarcini în care se observă procesul de formare a grupului și numai rezultatul este important. Sasan Bachka fără o diferență a fost mai întâi a căzut într-un sacru sau ultimul, dar este foarte important pentru el, în ce grup sa dovedit a fi în cele din urmă - printre cei care sunt în Sachka sau printre cei care sunt liberi.
2) Notă, folosim "și regula", deoarece Uniunea "și" este direct în descrierea evenimentului A, pentru care este necesar să se calculeze probabilitatea unei capturi comune a două grupuri. Cu toate acestea, îl aplicăm numai după ce au fost convinși de independența probelor. De fapt, nu poate Sazan, înotul spre saccu, recalculați colegii săi și spuneți lui Karpa: "rândul tău, deja două". Și crapul va fi de acord să urce în sacul lui Sazan? Dar dacă ar fi de acord, ar fi imposibil să se aplice această regulă. Ar fi necesar să se facă referire la conceptul de probabilitate condiționată.

Răspuns: 0,238.

Arată o decizie.

Dacă sunteți o școală absolventă și luați examenul, apoi după ce ați studiat această secțiune, întoarceți (10 pentru bază și 4 pentru nivelurile de profil ale EGE 2019 în matematică), care pot fi rezolvate folosind elementele combinatoricii și fără ea ( De exemplu, pentru a arunca monede). Care dintre modalitățile posibile de a rezolva sarcina vă place mai mult acum?

Și dacă doriți să cheltuiți mai mult în rezolvarea provocărilor combinatoricii pentru a afla cum să determinați rapid tipul de eșantionare și găsiți formulele dorite, apoi mergeți la pagină