Cum se adaugă logaritmi cu aceeași bază. Logaritmi: exemple și soluții

Expresii logaritmice, soluție de exemple. În acest articol vom analiza problemele legate de rezolvarea logaritmilor. În sarcini, se pune problema găsirii sensului expresiei. Trebuie remarcat faptul că conceptul de logaritm este utilizat în multe sarcini și este extrem de important să înțelegem semnificația acestuia. În ceea ce privește examenul, logaritmul este utilizat la rezolvarea ecuațiilor, la problemele aplicate, precum și la sarcinile legate de studiul funcțiilor.

Iată câteva exemple pentru a înțelege însăși semnificația logaritmului:


Identitate logaritmică de bază:

Proprietățile logaritmilor de reținut întotdeauna:

* Logaritmul produsului este suma logaritmilor factorilor.

* * *

* Logaritmul coeficientului (fracției) este egal cu diferența dintre logaritmii factorilor.

* * *

* Logaritmul puterii este egal cu produsul exponentului de către logaritmul bazei sale.

* * *

* Trecerea la o nouă bază

* * *

Mai multe proprietăți:

* * *

Calculul logaritmilor este strâns legat de utilizarea proprietăților exponenților.

Aici sunt câțiva dintre ei:

Esența acestei proprietăți este că atunci când numeratorul este transferat la numitor și invers, semnul exponentului se schimbă la opus. De exemplu:

Consecința acestei proprietăți:

* * *

Când ridicați o putere la o putere, baza rămâne aceeași, iar indicatorii sunt înmulțiți.

* * *

După cum puteți vedea, însăși conceptul de logaritm este simplu. Principalul lucru este că este nevoie de o bună practică, care oferă o anumită abilitate. Desigur, este necesară cunoașterea formulelor. Dacă abilitatea de a converti logaritmi elementari nu este formată, atunci când rezolvați sarcini simple, puteți face cu ușurință o greșeală.

Exersează, rezolvă mai întâi cele mai simple exemple de la cursul de matematică, apoi treci la altele mai dificile. În viitor, cu siguranță vă voi arăta cât de „urâți” se rezolvă logaritmii, nu vor exista astfel de examene, dar sunt de interes, nu ratați!

Asta e tot! Succes pentru tine!

Cu stimă, Alexander Krutitskikh

P.S: Aș fi recunoscător dacă ne-ați putea spune despre site pe rețelele de socializare.

Definiția logaritmului

Logaritmul lui b la baza a este exponentul la care trebuie ridicat a pentru a obține b.

Numărul e în matematică, se obișnuiește să se indice limita la care se exprimă

Numărul e este un număr irațional - un număr incomensurabil cu o unitate, nu poate fi exprimat cu precizie ca întreg sau fracționat raţional număr.

Scrisoare e - prima literă a unui cuvânt latin exponere - etalare, de unde și numele în matematică exponențială - functie exponentiala.

Număr e utilizate pe scară largă în matematică și în toate științele, într-un fel sau altul aplicând calcule matematice pentru nevoile lor.

Logaritmi. Proprietățile logaritmilor

Definiție: Logaritmul de bază al unui număr pozitiv b este exponentul c, la care trebuie ridicat numărul a pentru a obține numărul b.

Identitate logaritmică de bază:

7) Formula pentru trecerea la o nouă bază:

lna \u003d log e a, e ≈ 2.718 ...

Probleme și teste la tema „Logaritmi. Proprietățile logaritmilor "

  • Logaritmi - Subiecte importante pentru revizuirea utilizării în matematică

Pentru a finaliza cu succes sarcinile pe acest subiect, trebuie să cunoașteți definiția logaritmului, proprietățile logaritmilor, identitatea logaritmică de bază, definițiile logaritmului zecimal și natural. Principalele tipuri de probleme pe această temă sunt problemele de calcul și transformare a expresiilor logaritmice. Să luăm în considerare soluția lor în următoarele exemple.

Decizie: Folosind proprietățile logaritmilor, obținem

Decizie: folosind proprietățile gradului, obținem

1) (2 2) log 2 5 \u003d (2 log 2 5) 2 \u003d 5 2 \u003d 25

Proprietățile logaritmilor, formulărilor și dovezilor.

Logaritmii au o serie de proprietăți caracteristice. În acest articol, vom acoperi principalele proprietățile logaritmilor... Aici oferim formulările lor, notăm proprietățile logaritmilor sub formă de formule, prezentăm exemple de aplicare a acestora și dăm dovezi ale proprietăților logaritmilor.

Navigare în pagină.

Proprietăți de bază ale logaritmilor, formule

Pentru ușurarea memorării și a utilizării, reprezentăm proprietățile de bază ale logaritmilor ca o listă de formule. În paragraful următor, vom oferi formulările lor, dovezile, exemplele de utilizare și explicațiile necesare.

  • Proprietatea logaritmului unității: log a 1 \u003d 0 pentru orice a\u003e 0, a ≠ 1.
  • Logaritmul unui număr egal cu baza: log a a \u003d 1 pentru a\u003e 0, a ≠ 1.
  • Proprietatea logaritmului gradului de bază: log a a p \u003d p, unde a\u003e 0, a ≠ 1 și p este orice număr real.
  • Logaritmul produsului a două numere pozitive: log a (x y) \u003d log a x + log a y, a\u003e 0, a ≠ 1, x\u003e 0, y\u003e 0,
    și proprietatea logaritmului produsului de n numere pozitive: log a (x 1 x 2 ... xn) \u003d log ax 1 + log ax 2 + ... + log axn, a\u003e 0, a ≠ 1, x 1\u003e 0, x 2 \u003e 0,…, xn\u003e 0.
  • Proprietatea logaritmică a coeficientului: , unde a\u003e 0, a ≠ 1, x\u003e 0, y\u003e 0.
  • Logaritmul puterii unui număr: log a b p \u003d p · log a | b | , unde a\u003e 0, a ≠ 1, b și p sunt numere astfel încât gradul b p are sens și b p\u003e 0.
  • Corolar: , unde a\u003e 0, a ≠ 1, n este un număr natural mai mare decât unu, b\u003e 0.
  • Corolarul 1: , a\u003e 0, a ≠ 1, b\u003e 0, b ≠ 1.
  • Corolarul 2: , a\u003e 0, a ≠ 1, b\u003e 0, p și q sunt numere reale, q ≠ 0, în special, pentru b \u003d a avem .

    • Declarații și dovezi ale proprietăților

    Trecem la formularea și dovada proprietăților înregistrate ale logaritmilor. Toate proprietățile logaritmilor sunt dovedite pe baza definiției logaritmului și a identității logaritmice principale care rezultă din acesta, precum și a proprietăților gradului.

    Sa incepem cu proprietățile logaritmului unuia... Formularea sa este după cum urmează: logaritmul unu este zero, adică log a 1 \u003d 0 pentru orice a\u003e 0, a ≠ 1. Dovada este simplă: întrucât a 0 \u003d 1 pentru orice a care îndeplinește condițiile de mai sus a\u003e 0 și a ≠ 1, logul de egalitate a 1 \u003d 0 fiind dovedit imediat rezultă din definiția logaritmului.

    Să oferim exemple de aplicare a proprietății luate în considerare: log 3 1 \u003d 0, lg1 \u003d 0 și.

    Trecerea la următoarea proprietate: logaritmul unui număr de bază este unul, adică, log a a \u003d 1 pentru un\u003e 0, un ≠ 1. Într-adevăr, întrucât a 1 \u003d a pentru orice a, atunci prin definiția logaritmului log a a \u003d 1.

    Exemple de utilizare a acestei proprietăți de logaritmi sunt egalitățile log 5 5 \u003d 1, log 5.6 5.6 și lne \u003d 1.

    Logaritmul puterii unui număr egal cu baza logaritmului este egal cu exponentul... Această proprietate a logaritmului corespunde unei formule a formei log a a p \u003d p , unde a\u003e 0, a ≠ 1 și p este orice număr real. Această proprietate rezultă direct din definiția logaritmului. Rețineți că vă permite să indicați imediat valoarea logaritmului, dacă este posibil să reprezentați numărul sub semnul logaritmului sub forma unui grad de bază, vom vorbi mai multe despre acest lucru în articolul de calculare a logaritmilor.

    De exemplu, log 2 2 7 \u003d 7, lg10 -4 \u003d -4 și .

    Logaritmul produsului a două numere pozitive x și y este egal cu produsul logaritmilor acestor numere: log a (x y) \u003d log a x + log a y , a\u003e 0, a ≠ 1. Să dovedim proprietatea logaritmului produsului. În virtutea proprietăților gradului a log a x + log ay \u003d a log ax · a log ay, și întrucât prin identitatea logaritmică de bază un log ax \u003d x și un log ay \u003d y, atunci un log ax · a log ay \u003d x y. Astfel, un log a x + log a y \u003d x · y, de unde, prin definiția logaritmului, urmează egalitatea demonstrată.

    Să arătăm exemple de utilizare a proprietății logaritmului produsului: log 5 (2 3) \u003d log 5 2 + log 5 3 și .

    Proprietatea logaritmului produsului poate fi generalizată la produsul unui număr finit n de numere pozitive x 1, x 2, ..., x n ca log a (x 1 x 2 ... x n) \u003d log a x 1 + log a x 2 + ... + log a x n... Această egalitate poate fi dovedită fără probleme prin metoda inducției matematice.

    De exemplu, logaritmii naturali ai produsului pot fi înlocuiți cu suma celor trei logaritmi naturali ai numerelor 4, e și.

    Logaritmul coeficientului a două numere pozitive x și y este egală cu diferența dintre logaritmii acestor numere. Proprietatea logaritmului coeficientului corespunde unei formule a formei , unde a\u003e 0, a ≠ 1, x și y sunt câteva numere pozitive. Valabilitatea acestei formule este dovedită ca formulă pentru logaritmul produsului: din moment ce , apoi prin definiția logaritmului .

    Iată un exemplu de utilizare a acestei proprietăți a logaritmului: .

    Trecând la proprietatea logaritmului gradului... Logaritmul unei puteri este egal cu produsul exponentului de către logaritmul modulului bazei acestei puteri. Să scriem această proprietate a logaritmului gradului sub forma formulei: log a b p \u003d p · log a | b | , unde a\u003e 0, a ≠ 1, b și p sunt numere astfel încât gradul b p are sens și b p\u003e 0.

    În primul rând, dovedim această proprietate pentru b pozitiv. Identitatea logaritmică principală ne permite să reprezentăm numărul b ca un log a b, apoi b p \u003d (a log a b) p, iar expresia rezultată, datorită proprietății gradului, este egală cu un p log a b. Deci ajungem la egalitatea b p \u003d a p log a b, din care, prin definiția logaritmului, concluzionăm că log a b p \u003d p log a b.

    Rămâne să dovedim această proprietate pentru negativ b. Aici observăm că expresia log a b p pentru negativ b are sens doar pentru exponenții chiar p (deoarece valoarea exponentului b p trebuie să fie mai mare decât zero, altfel logaritmul nu va avea sens), iar în acest caz b p \u003d | b | p. Atunci b p \u003d | b | p \u003d (a log a | b |) p \u003d a p · log a | b | , de unde log a b p \u003d p · log a | b | ...

    De exemplu, și ln (-3) 4 \u003d 4 ln | -3 | \u003d 4 ln3.

    Proprietatea anterioară implică proprietatea logaritmului din rădăcină: logaritmul rădăcinii a n-a este egal cu produsul fracției 1 / n de logaritmul expresiei radicale, adică unde a\u003e 0, a ≠ 1, n este un număr natural mai mare decât unul, b\u003e 0.

    Dovada se bazează pe egalitate (a se vedea definiția exponentului fracțional), care este adevărat pentru orice b pozitiv și proprietatea logaritmului exponentului: .

    Iată un exemplu care utilizează această proprietate: .

    Acum să ne dovedim formula pentru trecerea la noua bază a logaritmului drăguț ... Pentru a face acest lucru, este suficient să se demonstreze egalitatea log c b \u003d log a b log c a. Identitatea logaritmică principală ne permite să reprezentăm numărul b ca un log a b, apoi log c b \u003d log c a log a b. Rămâne să se utilizeze proprietatea logaritmului gradului: log c a log a b \u003d log a b log c a. Așa a fost dovedit logul de egalitate c b \u003d log a b log c a și, prin urmare, s-a dovedit formula tranziției la noua bază a logaritmului .

    Să arătăm câteva exemple de aplicare a acestei proprietăți a logaritmilor: și .

    Formula pentru trecerea la o bază nouă vă permite să mergeți la lucru cu logaritmi care au o bază „convenabilă”. De exemplu, îl puteți folosi pentru a merge la logaritmi naturali sau zecimali, astfel încât să puteți calcula valoarea logaritmului din tabelul logaritmilor. Formula pentru trecerea la o nouă bază a unui logaritm permite, de asemenea, în unele cazuri să găsească valoarea unui logaritm dat atunci când sunt cunoscute valorile unor logaritmi cu alte baze.

    Este adesea folosit un caz special al formulei pentru tranziția la o nouă bază a logaritmului cu c \u003d b a formei. Aceasta arată că log a b și log b a sunt numere reciproc inverse. De exemplu, .

    De asemenea, se folosește adesea o formulă care este convenabilă pentru găsirea valorilor logaritmilor. Pentru a confirma cuvintele noastre, vom arăta cum este folosit pentru a calcula valoarea logaritmului formularului. Noi avem ... Pentru a dovedi formula, este suficient să folosiți formula pentru trecerea la noua bază a logaritmului a: .

    Rămâne să dovedim proprietățile comparației logaritmilor.

    Să folosim metoda prin contradicție. Să presupunem că pentru un 1\u003e 1, un 2\u003e 1 și un 1 2 și pentru 0 1, log a 1 b≤log a 2 b. Prin proprietățile logaritmilor, aceste inegalități pot fi rescrise ca și respectiv, și din ele rezultă că log b a 1 ≤log b a 2 și log b a 1 ≥log b a 2, respectiv. Apoi, conform proprietăților de grade cu aceleași baze, egalitățile b log b a 1 ≥b log b a 2 și b log b a 1 ≥b log b a 2 ar trebui să dețină, adică a 1 ≥a 2. Așa am ajuns la o contradicție cu condiția a 1 2. Aceasta completează dovada.

    Proprietățile de bază ale logaritmilor

    • Materiale de lecție
    • Descărcați toate formulele

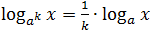
      • Logaritmii, ca orice numere, pot fi adăugate, scăzute și convertite în orice mod. Dar, din moment ce logaritmii nu sunt tocmai numere obișnuite, există reguli aici, care sunt numite proprietăți de bază.

      Este imperativ să cunoașteți aceste reguli - nicio problemă logaritmică gravă nu poate fi rezolvată fără ele. În plus, sunt foarte puține - totul poate fi învățat într-o singură zi. Deci sa începem.

      Adunarea și scăderea logaritmilor

      Luați în considerare două logaritmi cu aceleași baze: log a x și log a y. Apoi pot fi adăugate și scăzute și:

      Deci, suma logaritmilor este egală cu logaritmul produsului, iar diferența este logaritmul coeficientului. Vă rugăm să rețineți, punctul cheie aici este - temeiuri identice... Dacă motivele sunt diferite, aceste reguli nu funcționează!

      Aceste formule vă vor ajuta să calculați o expresie logaritmică chiar și atunci când părțile sale individuale nu sunt numărate (consultați lecția „Ce este un logaritm”). Aruncați o privire la exemple - și vedeți:

      O sarcină. Găsiți valoarea expresiei: log 6 4 + log 6 9.

      Deoarece bazele logaritmilor sunt aceleași, folosim formula sumă:
      log 6 4 + log 6 9 \u003d log 6 (4 9) \u003d log 6 36 \u003d 2.

      O sarcină. Găsiți valoarea expresiei: log 2 48 - log 2 3.

      Bazele sunt aceleași, folosim formula diferenței:
      log 2 48 - log 2 3 \u003d log 2 (48: 3) \u003d log 2 16 \u003d 4.

      O sarcină. Găsiți valoarea expresiei: log 3 135 - log 3 5.

      Din nou, bazele sunt aceleași, așa că avem:
      log 3 135 - log 3 5 \u003d log 3 (135: 5) \u003d log 3 27 \u003d 3.

      După cum puteți vedea, expresiile originale sunt compuse din logaritmi „răi”, care nu sunt numărați separat. Dar după transformări, se obțin numere complet normale. Multe teste se bazează pe acest fapt. Dar ce control - astfel de expresii cu toată seriozitatea (uneori - practic neschimbate) sunt oferite la examen.

      Eliminarea exponentului din logaritm

      Acum, să complicăm puțin sarcina. Ce se întâmplă dacă baza sau argumentul logaritmului se bazează pe un grad? Apoi exponentul acestui grad poate fi scos din semnul logaritmului conform următoarelor reguli:

    • log a x n \u003d n log a x;

      • Este ușor de văzut că ultima regulă urmează primele două. Dar este mai bine să ne amintim la fel - în unele cazuri va reduce semnificativ cantitatea de calcule.

      Desigur, toate aceste reguli au sens dacă se respectă ODL-ul logaritmului: a\u003e 0, a ≠ 1, x\u003e 0. Și încă un lucru: învățați să aplicați toate formulele nu numai de la stânga la dreapta, ci și invers, adică puteți introduce numerele din fața semnului logaritmului în logaritmul însuși. Aceasta este ceea ce este cel mai adesea necesar.

      O sarcină. Găsiți valoarea expresiei: log 7 49 6.

      Să scăpăm de gradul din argument folosind prima formulă:
      log 7 49 6 \u003d 6 log 7 49 \u003d 6 2 \u003d 12

      O sarcină. Găsiți semnificația expresiei:

      [Figura]

      Rețineți că numitorul conține logaritmul, a cărui bază și argumentul sunt puteri exacte: 16 \u003d 2 4; 49 \u003d 7 2. Noi avem:

      [Figura]

      Cred că ultimul exemplu are nevoie de o clarificare. Unde au dispărut logaritmii? Până în ultimul moment, lucrăm doar cu numitorul. Am prezentat baza și argumentul logaritmului care stătea acolo sub formă de grade și am scos indicatorii - am obținut o fracțiune „cu trei etaje”.

      Acum să ne uităm la fracția de bază. Numărătorul și numitorul conțin același număr: log 2 7. Deoarece log 2 7 ≠ 0, putem anula fracția - numitorul va rămâne 2/4. Conform regulilor aritmeticii, cele patru pot fi transferate la numărător, ceea ce a fost făcut. Rezultatul a fost răspunsul: 2.

      Trecerea la o nouă fundație

      Vorbind despre regulile pentru adunarea și scăderea logaritmilor, am subliniat în mod specific că acestea funcționează doar pentru aceleași baze. Ce se întâmplă dacă motivele sunt diferite? Ce se întâmplă dacă nu sunt puteri exacte ale aceluiași număr?

      Formule pentru trecerea la o nouă fundație vin în ajutor. Să le formulăm sub forma unei teoreme:

      Să se dea logaritmul jurnalul a x. Apoi, pentru orice număr c astfel încât c\u003e 0 și c ≠ 1, se menține următoarea egalitate:

      [Figura]

      În special, dacă punem c \u003d x, vom obține:

      [Figura]

      Din a doua formulă rezultă că este posibil să se schimbe baza și argumentul logaritmului, dar întreaga expresie este „inversată”, adică logaritmul apare în numitor.

      Aceste formule se găsesc rar în expresiile numerice convenționale. Este posibil să se evalueze cât de convenabile sunt acestea numai la rezolvarea ecuațiilor logaritmice și a inegalităților.

      Cu toate acestea, există sarcini care în general nu sunt rezolvate decât prin trecerea la o nouă fundație. Luați în considerare câteva dintre acestea:

      O sarcină. Găsiți valoarea expresiei: log 5 16 log 2 25.

      Rețineți că argumentele ambelor logaritmi conțin grade exacte. Să scoatem indicatorii: log 5 16 \u003d log 5 2 4 \u003d 4log 5 2; log 2 25 \u003d log 2 5 2 \u003d 2 log 2 5;

      Acum să „răsfoim” al doilea logaritm:

      [Figura]

      Deoarece produsul nu se schimbă de la permutarea factorilor, am înmulțit calm cei patru și doi, apoi am descoperit logaritmii.

      O sarcină. Găsiți valoarea expresiei: log 9 100 · lg 3.

      Baza și argumentul primului logaritm sunt grade exacte. Să scriem acest lucru și să scăpăm de valori:

      [Figura]

      Acum să scăpăm de logaritmul zecimal trecând la noua bază:

      [Figura]

      Identitate logaritmică de bază

      Adesea, în procesul de rezolvare, este necesar să se reprezinte un număr ca un logaritm la o bază dată. În acest caz, formulele ne vor ajuta:

    1. n \u003d log a a n

    2. În primul caz, numărul n devine exponentul în argument. Numărul n poate fi absolut orice, deoarece este doar valoarea logaritmului.

      A doua formulă este de fapt o definiție parafrazată. Se numește așa: identitate logaritmică de bază.

      De fapt, ce se întâmplă dacă numărul b este ridicat la o astfel de putere încât numărul b de la această putere să dea numărul a? Așa este: obțineți chiar acest număr a. Citiți din nou acest paragraf cu atenție - mulți oameni „atârnă” de el.

      La fel ca formulele pentru trecerea la o nouă bază, identitatea logaritmică de bază este uneori singura soluție posibilă.

      [Figura]

      Rețineți că log 25 64 \u003d log 5 8 - tocmai a mutat pătratul din bază și argumentul logaritm. Luând în considerare regulile pentru înmulțirea gradelor cu aceeași bază, obținem:

      [Figura]

      Dacă cineva nu știe, a fost o problemă reală la examen 🙂

      Unitate logaritmică și zero logaritmic

      În concluzie, voi da două identități care cu greu pot fi numite proprietăți - mai degrabă, acestea sunt consecințe ale definiției logaritmului. Ele sunt întâlnite în mod constant în probleme și, în mod surprinzător, creează probleme chiar și pentru studenții „avansați”.

      1. log a a \u003d 1 este unitatea logaritmică. Amintiți-vă odată pentru totdeauna: logaritmul pentru orice bază a din această bază este egal cu una.
      2. log a 1 \u003d 0 este zero logaritmic. Baza a poate fi orice, dar dacă argumentul este unul, logaritmul este zero! Deoarece un 0 \u003d 1 este o consecință directă a definiției.

      Asta-i toate proprietățile. Asigurați-vă că exersați punerea lor în practică! Descărcați foaia de trișare la începutul lecției, imprimați-o și rezolvați problemele.

      Logaritm. Proprietăți logaritmice (adunare și scădere).

      Proprietăți logaritmice urmează din definiția sa. Și deci logaritmul numărului b prin rațiune și este definit ca un indicator al gradului în care numărul trebuie crescut apentru a obține numărul b (doar numerele pozitive au logaritm).

      Din această formulare rezultă că calculul x \u003d log a b, este echivalent cu rezolvarea ecuației a x \u003d b. De exemplu, log 2 8 \u003d 3 deoarece 8 = 2 3 ... Formularea logaritmului face posibilă demonstrarea faptului că dacă b \u003d a c , apoi logaritmul numărului b prin rațiune a este egal din... De asemenea, este clar că subiectul logaritmului este strâns legat de subiectul puterii numărului.

      Cu logaritmii, ca și în cazul oricăror numere, puteți face operații de adunare, scădere și se transformă în orice mod posibil. Dar, datorită faptului că logaritmii nu sunt numere destul de obișnuite, aici se aplică reguli speciale, care sunt numite proprietăți de bază.

      Adunarea și scăderea logaritmilor.

      Să luăm două logaritmi cu aceleași baze: jurnal un x și log a y... Apoi eliminați este posibil să efectuați operații de adunare și scădere:

      După cum puteți vedea suma logaritmilor este egal cu logaritmul produsului și diferență logaritmi - logaritmul coeficientului. Mai mult, acest lucru este adevărat dacă numerele și, X și la pozitiv și a ≠ 1.

      Este important să fim atenți la faptul că principalul aspect al acestor formule este același motiv. Dacă motivele diferă între ele, aceste reguli nu se aplică!

      Regulile pentru adunarea și scăderea logaritmilor cu aceleași baze sunt citite nu numai de la stânga la dreapta, ci și înapoi. Ca rezultat, avem teoreme pentru logaritmul produsului și logaritmul coeficientului.

      Logaritmul produsului două numere pozitive este egal cu suma logaritmilor lor ; parafrazând această teoremă, obținem următoarele dacă numerele și, x și la pozitiv și a ≠ 1, apoi:

      Logaritmul coeficientului două numere pozitive este egală cu diferența dintre logaritmii dividendului și divizorul. Cu alte cuvinte, dacă numerele și, x și la pozitiv și a ≠ 1, apoi:

      Aplicăm teoremele de mai sus pentru a rezolva exemple:

      Dacă numerele x și la sunt negative atunci formula pentru logaritmul produsului devine lipsit de sens. Deci, este interzis să scrieți:

      deoarece expresiile log 2 (-8) și log 2 (-4) nu sunt deloc definite (funcție logaritmică la \u003d jurnal 2 x definit doar pentru valorile pozitive ale argumentului x).

      Teorema produsului aplicabil nu numai pentru doi, ci și pentru un număr nelimitat de factori. Aceasta înseamnă că pentru orice natură k și orice număr pozitiv x 1 , x 2 , . . . ,x nexistă o identitate:

      De teorema logaritmului puteți obține încă o proprietate a logaritmului. Este bine cunoscut că jurnalul A1 \u003d 0, deci

      Deci, egalitatea are loc:

      Logaritmi a două numere invers reciproce pe aceeași bază vor fi diferite unele de altele exclusiv prin semn. Asa de:

      Logaritm. Proprietățile logaritmilor

      Logaritm. Proprietățile logaritmilor

      Luați în considerare egalitatea. Spuneți-ne valorile și și dorim să găsim valoarea.

      Adică, căutăm un indicator al gradului în care trebuie să ne aruncăm pentru a ajunge.

      Lasa variabila poate lua orice valoare validă, apoi următoarele restricții sunt impuse variabilelor: o "title \u003d" a\u003e o "/\u003e, 1 ″ title \u003d” a1 ″ /\u003e, 0 ″ title \u003d ”b\u003e 0 ″ /\u003e

      Dacă cunoaștem valorile și și ne confruntăm cu sarcina de a găsi necunoscutul, atunci în acest scop este introdusă o acțiune matematică, care se numește logaritm.

      Pentru a găsi sensul, luăm logaritmul unui număr de bază :

      Logaritmul unui număr la bază este exponentul la care trebuie ridicat pentru a ajunge.

      adică identitate logaritmică de bază:

      o "title \u003d" a\u003e o "/\u003e, 1 ″ title \u003d” a1 ″ /\u003e, 0 ″ title \u003d ”b\u003e 0 ″ /\u003e

      este în esență o notație matematică definirea logaritmului.

      Prin urmare, operația matematică care ia logaritmul este inversa operației de exponențiere proprietățile logaritmilor strâns legată de proprietățile diplomei.

      Să enumerăm principalele proprietățile logaritmilor:

      (o "title \u003d" a\u003e o "/\u003e, 1 ″ title \u003d” a1 ″ /\u003e, 0 ″ title \u003d ”b\u003e 0 ″ /\u003e, 0,

      d\u003e 0 ″ /\u003e, 1 ″ title \u003d ”d1 ″ /\u003e

      4.

      5.

      Următorul grup de proprietăți vă permite să reprezentați exponentul unei expresii sub semnul logaritmului sau la baza logaritmului ca un coeficient înainte de semnul logaritmului:

      6.

      7.

      8.

      9.

      Următorul grup de formule vă permite să treceți de la un logaritm cu o bază dată la un logaritm cu o bază arbitrară și se numește formule de tranziție către o nouă bază:

      10.

      12. (corolar din proprietatea 11)

      Următoarele trei proprietăți nu sunt foarte cunoscute, dar sunt adesea folosite la rezolvarea ecuațiilor logaritmice sau la simplificarea expresiilor care conțin logaritmi:

      13.

      14.

      15.

      Cazuri speciale:

      — logaritm zecimal

      — logaritm natural

      La simplificarea expresiilor care conțin logaritmi, se aplică o abordare generală:

      1. Reprezentăm fracții zecimale ca fiind obișnuite.

      2. Reprezentăm numerele mixte ca fracții necorespunzătoare.

      3. Numerele de la baza logaritmului și sub semnul logaritmului sunt descompuse în factori primi.

      4. Încercăm să aducem toate logaritmii la o bază.

      5. Aplicați proprietățile logaritmilor.

      Să vedem câteva exemple de simplificare a expresiilor care conțin logaritmi.

      Exemplul 1.

      Calculati:

      Să simplificăm toți exponenții: sarcina noastră este de a le reduce la logaritmi, la baza cărora este același număr ca la baza gradului.

      \u003d\u003d (după proprietatea 7) \u003d (după proprietatea 6) \u003d

      Să înlocuim indicatorii pe care i-am obținut în expresia originală. Primim:

      Răspuns: 5.25

      Exemplul 2. Calculați:

      Să aducem toate logaritmii la baza 6 (în acest caz, logaritmii de la numitorul fracției se vor „muta” la numărător):

      Să descompunem numerele de sub semnul logaritmic în factori primi:

      Să aplicăm proprietățile 4 și 6:

      Să introducem înlocuitorul

      Primim:

      Raspunsul 1

      logaritm . Identitate logaritmică de bază.

      Proprietățile logaritmilor. Logaritm zecimal. Logaritm natural.

      logaritm numărul pozitiv N în bază (b > 0, b 1) este exponentul x la care trebuie crescut b pentru a obține N .

      Această intrare este echivalentă cu următoarea: b x \u003d N .

      Exemple: log 3 81 \u003d 4, deoarece 3 4 \u003d 81;

      log 1/3 27 \u003d – 3, deoarece (1/3) - 3 \u003d 3 3 \u003d 27.

      Definiția de mai sus a unui logaritm poate fi scrisă ca o identitate:

      Proprietățile de bază ale logaritmilor.

      2) jurnal 1 \u003d 0, din moment ce b 0 = 1 .

      3) Logaritmul produsului este egal cu suma logaritmilor factorilor:

      4) Logaritmul coeficientului este egal cu diferența dintre logaritmii dividendului și divizorului:

      5) Logaritmul puterii este egal cu produsul exponentului de către logaritmul bazei sale:

      Consecința acestei proprietăți este următoarea: logaritmul rădăcinii este egal cu logaritmul numărului rădăcinii împărțit la puterea rădăcinii:

      6) Dacă există un grad la baza logaritmului, atunci valoarea inversul exponentului poate fi scos pentru semnul rimei logaritmice:

      Ultimele două proprietăți pot fi combinate într-una singură:

      7) Formula modulului de tranziție (adică tranziția de la o bază a unui logaritm la o altă bază):

      Într-un caz particular, pentru N \u003d a noi avem:

      Logaritm zecimal denumit logaritm la bază 10. Este desemnat lg, adică jurnal 10 N \u003d lg N ... Logaritmi ai numerelor 10, 100, 1000 ,. p avna respectiv 1, 2, 3, ..., adică au atât de multe pozitive

      unități, câte zerouri sunt în logaritm după una. Logaritmi cu numere 0,1, 0,01, 0,001,. p sunt respectiv –1, –2, –3,…, adică au oricâte negative atât cât există zerouri în logaritmul din fața unuia (numărare și zero întregi). Logaritmele restului de numere au o parte fracționată numită mantisă... Se numește întreaga parte a logaritmului caracteristică... Logaritmele zecimale sunt cele mai convenabile pentru utilizare practică.

      Logaritmul natural denumit logaritm la bază e ... Este notat cu ln, adică Buturuga e N \u003d ln N ... Număr e este irațional, valoarea sa aproximativă este 2.718281828. Este limita la care numărul (1 + 1 / n) n cu creștere nelimitată n (cm. prima limită minunată (Consultați pagina Limitele secvențelor numerice).
      Oricât de ciudat ar părea, logaritmii naturali s-au dovedit a fi foarte convenabili pentru efectuarea diferitelor operațiuni legate de analiza funcțiilor. Calcularea logaritmelor de bază e desfășurat mult mai rapid decât în \u200b\u200borice altă bază.

    • De ce ai nevoie astăzi pentru a adopta un copil în Rusia? Adopția în Rusia, pe lângă o decizie personală responsabilă, implică o serie de proceduri pentru verificarea de către stat a candidaților. Selecția riguroasă în etapa pregătitoare contribuie la mai mult [...]
    • Informații gratuite în conformitate cu TIN sau OGRN din registrul fiscal în toată Rusia - online Pe portalul unificat al serviciilor fiscale, informații despre înregistrarea de către persoane juridice, întreprinzători individuali, [...]
    • Pedeapsa pentru conducere fără documente (permis de conducere, asigurare, STS) Uneori, din cauza uitării, șoferii ajung la volan fără VU și primesc o amendă pentru conducere fără documente. Amintim că un pasionat de mașini este obligat să fie alături de el [...]
    • Flori de oameni. Ce flori îi puteți oferi unui bărbat? Ce flori îi puteți oferi unui bărbat? Nu există atât de multe culori „masculine”, dar există unele care sunt date bărbaților. O mică listă florală în fața ta: Crizanteme. Trandafiri. Garoafe. [...]
    • O notă este o formă specială de document care este utilizată în mediul intern al unei întreprinderi și servește la rezolvarea rapidă a problemelor actuale de producție. De obicei, acest document este întocmit cu scopul de a introduce câteva [...]
    • Când și cum să obțineți partea finanțată a pensiei la Sberbank? Sberbank este o bancă parteneră a fondului de pensii de stat. Pe baza acestui fapt, cetățenii care au primit o pensie finanțată ar putea transfera partea finanțată către aceasta [...]
    • Alocații pentru copii în Ulyanovsk și regiunea Ulyanovsk în 2018 În plus, programele aprobate de legislația federală funcționează în toate regiunile. Să analizăm cine poate conta pe ce beneficii. Ca autorități regionale [...]
    • Îndrumări detaliate cu privire la modul de întocmire a unei procuri pentru a reprezenta interesele unei persoane în instanță Într-o cerere civilă sau de arbitraj, într-un dosar administrativ sau penal, interesele atât ale reclamantului, cât și ale pârâtului pot fi reprezentate de un avocat: [...]

    Logaritmul numărului N prin rațiune și numit exponent x la care vrei să construiești și pentru a obține numărul N

    Cu conditia ca
    ,
    ,

    Din definiția unui logaritm rezultă că
    , adică
    - această egalitate este identitatea logaritmică de bază.

    Logaritmii de bază 10 se numesc logaritmi zecimali. In schimb
    scrie
    .

    Logaritmi la bază e numit natural și notat
    .

    Proprietăți de bază ale logaritmelor.

      Logaritmul uneia pentru orice bază este zero

      Logaritmul produsului este egal cu suma logaritmilor factorilor.

    3) Logaritmul coeficientului este egal cu diferența logaritmelor


    Factor
    numit modulul de tranziție de la logaritmi la bază a la logaritmi la bază b .

    Folosind proprietățile 2-5, este adesea posibilă reducerea logaritmului unei expresii complexe la rezultatul operațiilor aritmetice simple peste logaritmi.

    De exemplu,

    Astfel de transformări ale logaritmului se numesc logaritmi. Transformările inverse la logaritm se numesc potențare.

    Capitolul 2. Elemente ale matematicii superioare.

    1. Limite

    Limita funcției
    este un număr finit A dacă, ca xx 0 pentru fiecare presetare
    , există un astfel de număr
    că odată
    apoi
    .

    O funcție care are o limită diferă de aceasta printr-o cantitate infinit de mică:
    , unde este un b.m.v., adică
    .

    Exemplu. Luați în considerare funcția
    .

    Când te străduiești
    , funcție y tinde spre zero:

    1.1. Teoreme de bază asupra limitelor.

      Limita unei valori constante este egală cu această valoare constantă

    .

      Limita sumei (diferenței) unui număr finit de funcții este egală cu suma (diferența) limitelor acestor funcții.

      Limita produsului unui număr finit de funcții este egală cu produsul limitelor acestor funcții.

      Limita coeficientului a două funcții este egală cu coeficientul limitelor acestor funcții dacă limita numitorului nu este zero.

    Limbe minunate

    ,
    Unde

    1.2. Exemple de calcul limită

    Cu toate acestea, nu toate limitele sunt ușor de calculat. Mai des, calculul limitei se reduce la dezvăluirea unei incertitudini precum: sau.

    .

    2. Derivată a funcției

    Să avem o funcție
    continuu pe segment
    .

    Argument am ceva creștere
    ... Apoi funcția va primi un increment
    .

    Valoarea argumentului corespunde valorii funcției
    .

    Valoarea argumentului
    corespunde valorii funcției.

    Prin urmare,.

    Să găsim limita acestui raport la
    ... Dacă această limită există, atunci se numește derivată a acestei funcții.

    Definiție 3 Derivată a acestei funcții
    după argument se numește limita raportului dintre creșterea unei funcții și creșterea argumentului, când creșterea argumentului tinde în mod arbitrar la zero.

    Derivată funcțională
    poate fi desemnat după cum urmează:

    ; ; ; .

    Definiție 4 Operația de găsire a derivatei unei funcții se numește diferenţiere.

    2.1. Semnificația mecanică a derivatului.

    Luați în considerare mișcarea rectilinie a unui corp rigid sau a unui punct material.

    Să la un moment dat în timp punct de mișcare
    era la distanță din poziția de plecare
    .

    După o anumită perioadă de timp
    se mișcă la distanță
    ... Atitudine =- viteza medie a unui punct material
    ... Să găsim limita acestui raport, ținând cont de faptul că
    .

    În consecință, determinarea vitezei instantanee a unui punct material se reduce la găsirea în timp a derivatei căii.

    2.2. Valoare geometrică derivată

    Să avem o funcție dată grafic
    .

    Figura: 1. Înțelesul geometric al derivatului

    În cazul în care un
    apoi punct
    , se va deplasa de-a lungul curbei, apropiindu-se de punct
    .

    prin urmare
    , adică valoarea derivatului dat valoarea argumentului numeric egal cu tangenta unghiului format de tangenta la un punct dat cu directia pozitiva a axei
    .

    2.3. Tabel cu formule de bază pentru diferențiere.

    Funcția de alimentare

    Functie exponentiala

    Funcția logaritmică

    Funcția trigonometrică

    Funcție trigonometrică inversă

    2.4. Reguli de diferențiere.

    Derivat de la

    Derivată a sumei (diferenței) funcțiilor


    Derivată a produsului a două funcții


    Derivată a coeficientului a două funcții


    2.5. Derivat dintr-o funcție complexă.

    Să funcția
    astfel încât să poată fi reprezentat ca

    și
    unde variabilă este un argument intermediar, atunci

    Derivata unei funcții complexe este egală cu produsul derivatei acestei funcții în raport cu argumentul intermediar prin derivata argumentului intermediar cu privire la x.

    Exemplul 1.

    Exemplul 2.

    3. Funcția diferențială.

    Să existe
    diferențiat pe un anumit segment
    lăsați-l să plece la această funcție are un derivat

    ,

    atunci putem scrie

    (1),

    unde - valoare infinit de mică,

    din moment ce la

    Înmulțind toți termenii egalității (1) cu
    noi avem:

    Unde
    - b.m.v. de ordin superior.

    Cantitatea
    se numește diferențialul funcției
    și notat

    .

    3.1. Valoarea geometrică a diferențialului.

    Să funcția
    .

    Fig. 2. Semnificația geometrică a diferențialului.

    .

    Este evident că diferențialul funcției
    este egal cu creșterea ordonatei tangentei în acest moment.

    3.2. Derivate și diferențiale ale diferitelor comenzi.

    Dacă există
    apoi
    numită prima derivată.

    Derivatul primului derivat se numește derivat de ordinul doi și este scris
    .

    Derivat al celui de-al nouălea ordin al funcției
    derivatul ordinului (n-1) este numit și este scris:

    .

    Diferențialul față de diferențialul unei funcții se numește diferențial al doilea sau diferențial de ordinul doi.

    .

    .

    3.3 Rezolvarea problemelor biologice folosind diferențierea.

    Sarcina 1. Studiile au arătat că creșterea unei colonii de microorganisme se supune legii
    Unde N - numărul de microorganisme (în mii), t –Timp (zile).

    b) Mărimea coloniei va crește sau va scădea în această perioadă?

    Răspuns. Colonia va crește ca mărime.

    Sarcina 2. Apa din lac este testată periodic pentru a controla conținutul de bacterii patogene. Prin t zile după testare, concentrația de bacterii este determinată de raport

    .

    Când va veni concentrația minimă de bacterii în lac și va fi posibil să înoți în el?

    SOLUȚIE O funcție atinge max sau min când derivata sa este zero.

    ,

    Să definim maxim sau min va fi în 6 zile. Pentru aceasta luăm a doua derivată.


    Răspuns: După 6 zile, va exista o concentrație minimă de bacterii.

    Urmată din definiția sa. Și deci logaritmul numărului b prin rațiune șieste definit ca un indicator al gradului în care numărul trebuie crescut apentru a obține numărul b (doar numerele pozitive au logaritm).

    Din această formulare rezultă că calculul x \u003d log a b, este echivalent cu rezolvarea ecuației a x \u003d b. De exemplu, log 2 8 \u003d 3deoarece 8 = 2 3 ... Formularea logaritmului face posibilă dovedirea că dacă b \u003d a c, apoi logaritmul numărului b prin rațiune a este egal din... Este de asemenea clar că subiectul logaritmului este strâns legat de subiectul puterii numărului.

    Cu logaritmii, ca și în cazul oricăror numere, puteți face operații de adunare, scădere și transformați în toate felurile posibile. Dar, având în vedere faptul că logaritmii nu sunt numere destul de obișnuite, aici se aplică propriile lor reguli speciale, care sunt numite proprietăți de bază.

    Adunarea și scăderea logaritmilor.

    Să luăm două logaritmi cu aceleași baze: jurnal un x și log a y... Apoi eliminați este posibil să efectuați operații de adunare și scădere:

    log a x + log a y \u003d log a (x y);

    log a x - log a y \u003d log a (x: y).

    log a(x 1 . x 2 . x 3 ... x k) = jurnal un x 1 + jurnal un x 2 + jurnal un x 3 + ... + log a x k.

    De teorema logaritmuluiputeți obține încă o proprietate a logaritmului. Este bine cunoscut că jurnalul A1 \u003d 0, deci

    buturuga A 1 / b\u003d jurnal A1 - jurnal a b\u003d - jurnal a b.

    Deci, egalitatea are loc:

    log a 1 / b \u003d - log a b.

    Logaritmi a două numere invers reciprocepe aceeași bază vor fi diferite unele de altele exclusiv prin semn. Asa de:

    Log 3 9 \u003d - log 3 1/9; log 5 1/125 \u003d -log 5 125.

    Instrucțiuni

    Notați expresia logaritmică specificată. Dacă expresia folosește logaritmul 10, notația sa este trunchiată și arată astfel: lg b este logaritmul zecimal. Dacă logaritmul are ca bază numărul e, atunci scrieți expresia: ln b - logaritm natural. Se înțelege că rezultatul oricărei este puterea la care trebuie ridicat numărul de bază pentru a obține numărul b.

    Când găsiți din suma a două funcții, trebuie doar să le diferențiați una câte una și să adăugați rezultatele: (u + v) "\u003d u" + v ";

    Când găsiți derivata produsului a două funcții, este necesar să înmulțiți derivata primei funcții cu a doua și să adăugați derivata celei de-a doua funcții, înmulțită cu prima funcție: (u * v) "\u003d u" * v + v "* u;

    Pentru a găsi derivata coeficientului a două funcții, este necesar, din produsul derivatei dividendului înmulțit cu funcția divizor, să se scadă produsul derivatei divizorului înmulțit cu funcția dividendului și să se împartă toate acestea la funcția divizorului pătrat. (u / v) "\u003d (u" * v-v "* u) / v ^ 2;

    Dacă este dată o funcție complexă, atunci este necesar să se înmulțească derivata funcției interne și derivata celei externe. Fie y \u003d u (v (x)), apoi y "(x) \u003d y" (u) * v "(x).

    Folosind cele obținute mai sus, puteți diferenția aproape orice funcție. Așadar, să ne uităm la câteva exemple:

    y \u003d x ^ 4, y "\u003d 4 * x ^ (4-1) \u003d 4 * x ^ 3;

    y \u003d 2 * x ^ 3 * (e ^ xx ^ 2 + 6), y "\u003d 2 * (3 * x ^ 2 * (e ^ xx ^ 2 + 6) + x ^ 3 * (e ^ x-2 * X));
    Există, de asemenea, probleme pentru calcularea derivatei la un punct. Fie ca funcția y \u003d e ^ (x ^ 2 + 6x + 5) să fie dată, trebuie să găsiți valoarea funcției în punctul x \u003d 1.
    1) Găsiți derivata funcției: y "\u003d e ^ (x ^ 2-6x + 5) * (2 * x +6).

    2) Calculați valoarea funcției la punctul dat y "(1) \u003d 8 * e ^ 0 \u003d 8

    Videoclipuri similare

    Sfat util

    Aflați tabelul derivatelor elementare. Acest lucru va economisi semnificativ timp.

    surse:

    • derivată a unei constante

    Deci, care este diferența dintre o ecuație irațională și una rațională? Dacă variabila necunoscută se află sub semnul rădăcinii pătrate, atunci ecuația este considerată irațională.

    Instrucțiuni

    Principala metodă pentru soluționarea unor astfel de ecuații este metoda de construire a ambelor părți ecuaţiile într-un pătrat. In orice caz. acest lucru este firesc, primul pas este să scapi de semn. Această metodă nu este dificilă din punct de vedere tehnic, dar uneori poate avea probleme. De exemplu, ecuația v (2x-5) \u003d v (4x-7). Pătrând ambele părți ale acestuia, obțineți 2x-5 \u003d 4x-7. Această ecuație nu va fi greu de rezolvat; x \u003d 1. Numărul 1 nu va fi dat ecuaţiile... De ce? Înlocuiți 1 în ecuația pentru x, iar ambele părți din dreapta și din stânga vor conține expresii care nu au sens, adică. Această valoare nu este validă pentru o rădăcină pătrată. Prin urmare, 1 este o rădăcină străină și, prin urmare, ecuația dată nu are rădăcini.

    Deci, o ecuație irațională este rezolvată folosind metoda de a pătrat ambele părți ale acesteia. Și după ce am rezolvat ecuația, este imperativ să tăiem rădăcinile străine. Pentru a face acest lucru, înlocuiți rădăcinile găsite în ecuația inițială.

    Luați în considerare un altul.
    2x + vx-3 \u003d 0
    Desigur, această ecuație poate fi rezolvată în același mod ca și cea precedentă. Mutați compozitul ecuaţiilecare nu au o rădăcină pătrată în partea dreaptă și apoi folosesc metoda de pătrat. rezolvați ecuația și rădăcinile raționale rezultate. Dar alta, mai elegantă. Introduceți o nouă variabilă; vx \u003d y. În consecință, obțineți o ecuație de forma 2y2 + y-3 \u003d 0. Adică ecuația pătratică obișnuită. Găsește-i rădăcinile; y1 \u003d 1 și y2 \u003d -3 / 2. Apoi, decideți două ecuaţiile vx \u003d 1; vx \u003d -3 / 2. A doua ecuație nu are rădăcini, din prima găsim că x \u003d 1. Nu uitați să verificați rădăcinile.

    Rezolvarea identităților este suficient de ușoară. Aceasta necesită transformări identice până la atingerea obiectivului. Astfel, cu ajutorul celor mai simple operații aritmetice, sarcina va fi rezolvată.

    Vei avea nevoie

    • - hârtie;
    • - un stilou.

    Instrucțiuni

    Cele mai simple astfel de transformări sunt înmulțirea prescurtată algebrică (cum ar fi pătratul sumei (diferența), diferența de pătrate, suma (diferența), cubul sumei (diferența)). În plus, există multe și formule trigonometrice, care sunt în esență aceleași identități.

    Într-adevăr, pătratul sumei a doi termeni este egal cu pătratul primului plus de două ori produsul primului cu cel de-al doilea și plus pătratul celui de al doilea, adică (a + b) ^ 2 \u003d (a + b) (a + b) \u003d a ^ 2 + ab + ba + b ^ 2 \u003d a ^ 2 + 2ab + b ^ 2.

    Simplificați ambele

    Principii generale de soluționare

    Revizuirea printr-un manual despre calcul sau matematică superioară, care este o integrală definitivă. După cum știți, soluția unei integrale definite este o funcție, a cărei derivată va da integrandului. Această funcție se numește antiderivativ. Integralele de bază sunt construite conform acestui principiu.
    Determinați după tipul integrandului, care dintre integralele tabulare este potrivită în acest caz. Nu este întotdeauna posibil să se determine imediat acest lucru. Adesea, vizualizarea tabelară devine vizibilă numai după mai multe transformări pentru a simplifica integrandul.

    Metoda de înlocuire variabilă

    Dacă integrandul este o funcție trigonometrică, în al cărei argument există un polinom, atunci încercați să utilizați metoda schimbării variabile. Pentru a face acest lucru, înlocuiți polinomul din argumentul integrandului cu o variabilă nouă. Determinați noile limite de integrare din relația dintre variabila nouă și cea veche. Prin diferențierea acestei expresii, găsiți noul diferențial în. Astfel, veți obține o nouă formă a integralei anterioare, apropiată sau chiar corespunzătoare unei tabulare.

    Soluție de integrale de tipul al doilea

    Dacă integrala este o integrantă a celui de-al doilea tip, forma vectorială a integrandului, atunci va trebui să utilizați regulile pentru trecerea de la aceste integrale la cele scalare. Una dintre aceste reguli este raportul Ostrogradsky-Gauss. Această lege permite trecerea de la fluxul de rotor al unei anumite funcții vectoriale la o triplă integrală față de divergența unui câmp vector dat.

    Înlocuirea limitelor integrării

    După găsirea antiderivativului, este necesar să se substituie limitele integrării. Mai întâi conectați valoarea limită superioară la expresia antiderivativă. Veți obține un număr. În continuare, scade din numărul rezultat un alt număr obținut de la limita inferioară la antiderivativ. Dacă una dintre limitele integrării este infinitul, atunci când o substituiți în funcția antiderivativă, este necesar să mergeți la limită și să găsiți la ce tinde expresia.
    Dacă integrala este bidimensională sau tridimensională, atunci va trebui să reprezentați geometric limitele integrării pentru a înțelege cum să calculați integrala. Într-adevăr, în cazul unei integrale tridimensionale, să zicem, limitele integrării pot fi planuri întregi care leagă volumul care trebuie integrat.