Nedefinovaný slough. Systém rovnic
Systém lineárních rovnic je spojením n lineárních rovnic, z nichž každá obsahuje k proměnných. Píše se to takto:
Mnoho lidí, kteří se poprvé setkali s vyšší algebrou, se mylně domnívá, že počet rovnic se musí nutně shodovat s počtem proměnných. Ve školní algebře se to obvykle stává, ale pro vyšší algebru to obecně řečeno neplatí.
Řešením soustavy rovnic je posloupnost čísel (k 1, k 2, ..., k n), která je řešením každé rovnice soustavy, tzn. při dosazení do této rovnice místo proměnných x 1, x 2, ..., x n dává správnou číselnou rovnost.
Řešení soustavy rovnic tedy znamená najít množinu všech jejích řešení nebo dokázat, že tato množina je prázdná. Protože se počet rovnic a počet neznámých nemusí shodovat, jsou možné tři případy:
- Systém je nekonzistentní, tzn. množina všech řešení je prázdná. Poměrně vzácný případ, který lze snadno odhalit bez ohledu na metodu použitou k řešení systému.
- Systém je konzistentní a definovaný, tzn. má přesně jedno řešení. Klasická verze, známá již ze školy.
- Systém je konzistentní a nedefinovaný, tzn. má nekonečně mnoho řešení. Toto je nejtěžší varianta. Nestačí poukázat na to, že „systém má nekonečnou množinu řešení“ – je třeba popsat, jak je tato množina uspořádána.
Proměnná x i se nazývá povolená, pokud je zahrnuta pouze v jedné rovnici systému a s koeficientem 1. Jinými slovy, ve zbývajících rovnicích musí být koeficient u proměnné x i roven nule.
Pokud v každé rovnici zvolíme jednu povolenou proměnnou, dostaneme množinu povolených proměnných pro celý systém rovnic. Samotný systém, napsaný v této podobě, bude také nazýván povoleným. Obecně lze říci, že jeden a tentýž počáteční systém lze redukovat na různé povolené, ale to už je nám jedno. Zde jsou příklady povolených systémů:
Oba systémy jsou povoleny s ohledem na proměnné x 1, x 3 a x 4. Nicméně se stejným úspěchem lze tvrdit, že druhý systém je povolen s ohledem na x 1, x 3 a x 5. Poslední rovnici stačí přepsat jako x 5 = x 4.
Podívejme se nyní na obecnější případ. Předpokládejme, že máme k proměnných, z nichž r je povoleno. Pak jsou možné dva případy:
- Počet povolených proměnných r se rovná celkovému počtu proměnných k: r = k. Získáme systém k rovnic, ve kterých r = k povolených proměnných. Takový systém je společný a určitý, protože x 1 = b 1, x 2 = b 2, ..., x k = b k;
- Počet povolených proměnných r je menší než celkový počet proměnných k:r< k . Остальные (k − r ) переменных называются свободными - они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.
Takže ve výše uvedených systémech jsou proměnné x 2, x 5, x 6 (pro první systém) a x 2, x 5 (pro druhý) volné. Případ, kdy existují volné proměnné, je nejlépe formulovat jako věta:
Upozornění: toto je velmi důležitý bod! V závislosti na tom, jak napíšete výsledný systém, může být stejná proměnná povolena i volná. Většina vyšších učitelů matematiky doporučuje zapisovat proměnné v lexikografickém pořadí, tzn. vzestupný index. Touto radou se však nemusíte vůbec řídit.
Teorém. Pokud jsou v systému n rovnic povoleny proměnné x 1, x 2, ..., x r a x r + 1, x r + 2, ..., x k jsou volné, pak:
- Pokud nastavíme hodnoty na volné proměnné (xr + 1 = tr + 1, xr + 2 = tr + 2, ..., xk = tk) a pak najdeme hodnoty x 1, x 2, .. ., xr, dostaneme jedno z řešení.
- Pokud se ve dvou řešeních shodují hodnoty volných proměnných, shodují se i hodnoty povolených proměnných, tzn. řešení jsou stejná.
Jaký je význam této věty? K získání všech řešení řešené soustavy rovnic stačí vybrat volné proměnné. Poté přiřazením různých hodnot k volným proměnným získáme hotová řešení. To je vše - tímto způsobem můžete získat všechna řešení systému. Jiná řešení nejsou.
Závěr: vyřešená soustava rovnic je vždy konzistentní. Je-li počet rovnic v řešeném systému roven počtu proměnných, bude systém určitý, je-li menší, bude neurčitý.
A všechno by bylo v pořádku, ale nabízí se otázka: jak získat vyřešenou z původní soustavy rovnic? Pro toto existuje
Obsah lekceLineární rovnice ve dvou proměnných
Student má 200 rublů na oběd ve škole. Dort stojí 25 rublů a šálek kávy stojí 10 rublů. Kolik dortů a šálků kávy si můžete koupit za 200 rublů?
Označme počet dortů podle X a počet šálků kávy poté y... Potom bude cena dortů označena výrazem 25 X a náklady na šálky kávy po 10 y .
25X - cena X pečivo
10y - cena yšálky kávy
Celková částka by měla být 200 rublů. Pak dostaneme rovnici se dvěma proměnnými X a y
25X+ 10y= 200
Kolik kořenů má tato rovnice?
Vše závisí na chuti studenta. Pokud si koupí 6 koláčů a 5 šálků kávy, kořeny rovnice budou 6 a 5.
O páru hodnot 6 a 5 se říká, že jsou kořeny rovnice 25 X+ 10y= 200. Zapisuje se jako (6; 5), přičemž první číslo je hodnota proměnné X a druhá je hodnota proměnné y .
6 a 5 nejsou jediné kořeny, které obracejí rovnici 25 X+ 10y= 200 na identitu. V případě potřeby si student může koupit 4 koláče a 10 šálků kávy za stejných 200 rublů:
V tomto případě kořeny rovnice 25 X+ 10y= 200 je dvojice hodnot (4; 10).
Kromě toho si student nemůže koupit kávu vůbec, ale koupit koláče za všech 200 rublů. Pak kořeny rovnice 25 X+ 10y= 200 budou hodnoty 8 a 0
Nebo naopak, nekupujte dorty, ale kupujte kávu za všech 200 rublů. Pak kořeny rovnice 25 X+ 10y= 200 budou hodnoty 0 a 20
Zkusme vyjmenovat všechny možné kořeny rovnice 25 X+ 10y= 200. Shodněme se, že hodnoty X a y patří do množiny celých čísel. A nechť jsou tyto hodnoty větší nebo rovné nule:
X∈Z y∈ Z;
x ≥ 0, y ≥ 0
Takže to bude výhodné pro samotného studenta. Je výhodnější koupit dorty celé než například několik celých dortů a půl dortu. Je také pohodlnější brát kávu v celých šálcích než například několik celých šálků a půl šálku.
Všimněte si, že pro liché X je nemožné dosáhnout rovnosti za žádných y... Pak hodnoty X budou následující čísla 0, 2, 4, 6, 8. A vědět X můžete snadno určit y
Tak jsme dostali následující páry hodnot (0; 20), (2; 15), (4; 10), (6; 5), (8; 0). Tyto dvojice jsou řešeními nebo kořeny rovnice 25 X+ 10y= 200. Dělají z této rovnice identitu.
Rovnice formuláře ax + by = c se nazývají lineární rovnice ve dvou proměnných... Řešení nebo kořeny této rovnice se nazývá dvojice hodnot ( X; y), což z něj dělá identitu.
Všimněte si také, že pokud je lineární rovnice ve dvou proměnných zapsána ve tvaru ax + b y = c, pak říkají, že je to napsané kanonický(normální) forma.
Některé lineární rovnice ve dvou proměnných lze redukovat na kanonickou formu.
Například rovnice 2(16X+ 3y - 4) = 2(12 + 8X − y) lze zredukovat na formu ax + by = c... Rozbalením závorek na obou stranách této rovnice získáme 32X + 6y − 8 = 24 + 16X − 2y ... Členy obsahující neznámé seskupujeme na levé straně rovnice a členy bez neznámých - na pravé straně. Pak dostaneme 32X - 16X+ 6y+ 2y = 24 + 8 ... Při podobných členech v obou částech dostaneme rovnici 16 X+ 8y= 32. Tato rovnice je redukována do tvaru ax + by = c a je kanonický.
Dříve zvažovaná rovnice 25 X+ 10y= 200 je také lineární rovnice dvou proměnných v kanonickém tvaru. V této rovnici parametry A , b a C se rovnají hodnotám 25, 10 a 200.
Vlastně rovnice ax + by = c má nespočet řešení. Řešení rovnice 25X+ 10y= 200, jeho kořeny jsme hledali pouze na množině celých čísel. V důsledku toho bylo získáno několik párů hodnot, které z této rovnice učinily identitu. Ale na množině racionálních čísel rovnice 25 X+ 10y= 200 bude mít nespočet řešení.
Chcete-li získat nové páry hodnot, musíte použít libovolnou hodnotu pro X pak vyjádřit y... Vezměme si například proměnnou X hodnota 7. Pak dostaneme rovnici s jednou proměnnou 25 × 7 + 10y= 200 ve kterém se můžete vyjádřit y
Nech být X= 15. Pak rovnice 25X+ 10y= 200 bude mít tvar 25 × 15 + 10y= 200. Z toho zjistíme, že y = −17,5
Nech být X= −3. Pak rovnice 25X+ 10y= 200 bude mít tvar 25 × (−3) + 10y= 200. Z toho zjistíme, že y = −27,5
Soustava dvou lineárních rovnic ve dvou proměnných
Pro rovnici ax + by = c můžete použít libovolné hodnoty X a najít hodnoty pro y... Vzato samostatně, bude mít taková rovnice nespočet řešení.
Ale také se stává, že proměnné X a y souvisí nikoli jednou, ale dvěma rovnicemi. V tomto případě tvoří tzv soustava lineárních rovnic ve dvou proměnných... Takový systém rovnic může mít jeden pár hodnot (nebo jinými slovy: „jedno řešení“).
Může se také stát, že systém nemá vůbec žádná řešení. Systém lineárních rovnic může mít ve vzácných a výjimečných případech nespočetné množství řešení.
Dvě lineární rovnice tvoří systém, kdy hodnoty X a y jsou zahrnuty v každé z těchto rovnic.
Vraťme se k úplně první rovnici 25 X+ 10y= 200. Jednou z dvojic hodnot pro tuto rovnici byla dvojice (6; 5). To je případ, kdy jste si mohli koupit 6 koláčů a 5 šálků kávy za 200 rublů.
Formulujme úlohu tak, aby se dvojice (6; 5) stala jediným řešením rovnice 25 X+ 10y= 200. K tomu sestavíme další rovnici, která by se vztahovala ke stejnému X koláče a yšálky kávy.
Nastavíme text problému takto:
„Školák koupil několik dortů a několik šálků kávy za 200 rublů. Dort stojí 25 rublů a šálek kávy stojí 10 rublů. Kolik dortů a šálků kávy koupil školák, pokud je známo, že počet dortů je o jeden větší než počet šálků kávy?"
První rovnici už máme. Tato rovnice je 25 X+ 10y= 200. Nyní udělejme rovnici pro podmínku "Počet dortů je o jeden větší než počet šálků kávy" .
Počet dortů je X, a počet šálků kávy je y... Tuto frázi můžete napsat pomocí rovnice x - y= 1. Tato rovnice by znamenala, že rozdíl mezi dorty a kávou je 1.
x = y+ 1. Tato rovnice znamená, že počet dortů je o jeden větší než počet šálků kávy. Pro dosažení rovnosti se k počtu šálků kávy přidá jedna. To lze snadno pochopit, pokud použijeme model vah, který jsme uvažovali při studiu nejjednodušších problémů:
Máme dvě rovnice: 25 X+ 10y= 200 a x = y+ 1. Vzhledem k tomu, že hodnoty X a y, konkrétně 6 a 5 jsou zahrnuty v každé z těchto rovnic, pak dohromady tvoří systém. Pojďme si tento systém zapsat. Pokud rovnice tvoří systém, pak jsou orámovány znakem systému. Systémovým znakem je složená závorka:
Pojďme vyřešit tento systém. To nám umožní vidět, jak se dostáváme k hodnotám 6 a 5. Existuje mnoho metod pro řešení takových systémů. Podívejme se na ty nejoblíbenější.
Substituční metoda
Název této metody mluví sám za sebe. Její podstatou je dosazení jedné rovnice do druhé, která předtím vyjádřila jednu z proměnných.
V našem systému není potřeba nic vyjadřovat. Ve druhé rovnici X = y+ 1 proměnná X již vyjádřeno. Tato proměnná se rovná výrazu y+ 1. Pak můžete tento výraz nahradit v první rovnici místo proměnné X
Po substituci výrazu y+ 1 k první rovnici místo X, dostaneme rovnici 25(y+ 1) + 10y= 200 ... Je to lineární rovnice s jednou proměnnou. Tato rovnice je poměrně jednoduchá na řešení:
Zjistili jsme hodnotu proměnné y... Nyní tuto hodnotu dosadíme do jedné z rovnic a najdeme hodnotu X... K tomu je vhodné použít druhou rovnici X = y+ 1. V něm dosadíme hodnotu y
To znamená, že dvojice (6; 5) je řešením soustavy rovnic, jak jsme zamýšleli. Zkontrolujeme a ujistíme se, že dvojice (6; 5) vyhovuje systému:
Příklad 2
Dosaďte první rovnici X= 2 + y do druhé rovnice 3 X - 2y= 9. V první rovnici proměnná X se rovná 2 + y... Tento výraz dosadíme do druhé rovnice místo X
Nyní najdeme hodnotu X... Chcete-li to provést, nahraďte hodnotu y do první rovnice X= 2 + y
Řešením systému je tedy hodnota páru (5; 3)
Příklad 3... Vyřešte následující soustavu rovnic substituční metodou:
Zde na rozdíl od předchozích příkladů není jedna z proměnných explicitně vyjádřena.
Chcete-li nahradit jednu rovnici jinou, musíte nejprve.
Je žádoucí vyjádřit proměnnou, která má koeficient jedna. Koeficient jedna má proměnnou X která je obsažena v první rovnici X+ 2y= 11. Tuto proměnnou vyjádříme.
Po proměnné výraz X, náš systém bude mít následující podobu:
Nyní dosadíme první rovnici do druhé a zjistíme hodnotu y
Náhradní y X
Řešením systému je tedy dvojice hodnot (3; 4)
Samozřejmě můžete vyjádřit i proměnnou y... Kořeny se od toho nezmění. Ale pokud se vyjádříte y, dostanete ne tak jednoduchou rovnici, jejíž řešení zabere více času. Bude to vypadat takto:
Vidíme to na tomto příkladu vyjádřit X mnohem pohodlnější než vyjádření y .
Příklad 4... Vyřešte následující soustavu rovnic substituční metodou:
Vyjádřeme se v první rovnici X... Poté bude mít systém podobu:
y
Náhradní y do první rovnice a najděte X... Můžete použít původní rovnici 7 X+ 9y= 8, nebo použijte rovnici, ve které je proměnná vyjádřena X... Použijeme tuto rovnici, jak je to vhodné:
Řešením systému je tedy dvojice hodnot (5; −3)
Způsob sčítání
Metodou sčítání je sčítání rovnic v soustavě člen po členu. Toto přidání vede k tomu, že se vytvoří nová rovnice s jednou proměnnou. A vyřešit takovou rovnici je docela jednoduché.
Pojďme řešit následující soustavu rovnic:
Přidejte levou stranu první rovnice k levé straně druhé rovnice. A pravá strana první rovnice s pravou stranou druhé rovnice. Dostaneme následující rovnost:
Zde jsou podobné termíny:
Ve výsledku jsme dostali nejjednodušší rovnici 3 X= 27, jehož kořen je 9. Znát hodnotu X můžete najít hodnotu y... Nahraďte hodnotu X do druhé rovnice x - y= 3. Dostáváme 9- y= 3. Odtud y= 6 .
To znamená, že řešením systému je dvojice hodnot (9; 6)
Příklad 2
Přidejte levou stranu první rovnice k levé straně druhé rovnice. A pravá strana první rovnice s pravou stranou druhé rovnice. Ve výsledné rovnosti uvádíme podobné pojmy:
Ve výsledku jsme dostali nejjednodušší rovnici 5 X= 20, jehož odmocnina je 4. Znát hodnotu X můžete najít hodnotu y... Nahraďte hodnotu X do první rovnice 2 x + y= 11. Dostáváme 8+ y= 11. Odtud y= 3 .
Řešením systému je tedy dvojice hodnot (4; 3)
Proces přidávání není podrobně popsán. Musí to být provedeno v mysli. Navíc musí být obě rovnice zredukovány na kanonickou formu. To znamená ac + by = c .
Z uvažovaných příkladů je vidět, že hlavním účelem sčítání rovnic je zbavit se jedné z proměnných. Ale ne vždy je možné okamžitě vyřešit soustavu rovnic sčítací metodou. Nejčastěji je systém předběžně uveden do formy, ve které můžete přidat rovnice obsažené v tomto systému.
Například systém 
lze okamžitě vyřešit sčítací metodou. Při sečtení obou rovnic jsou členy y a −y zmizí, protože jejich součet je nula. Výsledkem je nejjednodušší rovnice 11 X= 22, jehož odmocnina je 2. Pak bude možné určit y rovný 5.
A soustava rovnic 
metodu sčítání nelze vyřešit okamžitě, protože to nepovede ke zmizení jedné z proměnných. Výsledkem sčítání bude rovnice 8 X+ y= 28, který má nespočet řešení.
Pokud se obě strany rovnice vynásobí nebo vydělí stejným číslem, které se nerovná nule, získá se rovnice, která je ekvivalentní dané. Toto pravidlo platí i pro soustavu lineárních rovnic ve dvou proměnných. Jednu z rovnic (nebo obě rovnice) lze vynásobit nějakým číslem. Výsledkem bude ekvivalentní systém, jehož kořeny se budou shodovat s předchozím.
Vraťme se k úplně prvnímu systému, který popisoval, kolik dortů a šálků kávy si student koupil. Řešením tohoto systému byla dvojice hodnot (6; 5).
Vynásobme obě rovnice v této soustavě nějakými čísly. Řekněme, že první rovnice je vynásobena 2 a druhá 3
V důsledku toho jsme získali systém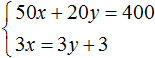 
Řešením tohoto systému je stále dvojice hodnot (6; 5)
To znamená, že rovnice obsažené v systému lze zredukovat na formu vhodnou pro aplikaci sčítací metody.
Zpět k systému , kterou jsme nedokázali vyřešit sčítací metodou.
Vynásobte první rovnici 6 a druhou −2
Pak dostaneme následující systém:
Sečteme rovnice obsažené v tomto systému. Přidání komponent 12 X a -12 X výsledkem bude 0, sčítání 18 y a 4 y dá 22 y a sečtením 108 a −20 dostaneme 88. Pak dostaneme rovnici 22 y= 88, tedy y = 4 .
Pokud je zpočátku obtížné přidávat rovnice ve vaší mysli, můžete si zapsat, jak se levá strana první rovnice přidá k levé straně druhé rovnice a pravá strana první rovnice k pravé strana druhé rovnice:
S vědomím, že hodnota proměnné y je 4, můžete najít hodnotu X... Náhradní y do jedné z rovnic, například do první rovnice 2 X+ 3y= 18. Pak dostaneme rovnici s jednou proměnnou 2 X+ 12 = 18. Přesuňte 12 na pravou stranu, změňte znaménko, dostaneme 2 X= 6, tedy X = 3 .
Příklad 4... Vyřešte následující soustavu rovnic metodou sčítání:
Vynásobte druhou rovnici −1. Poté bude mít systém následující podobu:
Sečteme obě rovnice. Přidávání komponent X a −x výsledkem bude 0, sčítání 5 y a 3 y dá 8 y a sečtením 7 a 1 dostaneme 8. Výsledkem je rovnice 8 y= 8, jehož kořen je 1. S vědomím, že hodnota y je rovna 1, můžete najít hodnotu X .
Náhradní y do první rovnice, dostaneme X+ 5 = 7, tedy X= 2
Příklad 5... Vyřešte následující soustavu rovnic metodou sčítání:
Je žádoucí, aby termíny obsahující stejné proměnné byly umístěny pod sebou. Proto ve druhé rovnici jsou členy 5 y a -2 X vyměnit místa. V důsledku toho bude mít systém podobu:
Vynásobme druhou rovnici 3. Pak bude systém mít tvar:
Nyní sečteme obě rovnice. Výsledkem sčítání dostaneme rovnici 8 y= 16, jehož kořen je 2.
Náhradní y do první rovnice dostaneme 6 X-14 = 40. Posuňte člen −14 na pravou stranu, změnou znaménka dostaneme 6 X= 54. Odtud X= 9.
Příklad 6... Vyřešte následující soustavu rovnic metodou sčítání:
Zbavme se zlomků. Vynásobte první rovnici 36 a druhou 12
Ve výsledném systému 
první rovnici lze vynásobit −5 a druhou 8
Ve výsledné soustavě sečteme rovnice. Pak dostaneme nejjednodušší rovnici −13 y= -156. Odtud y= 12. Náhradní y do první rovnice a najděte X
Příklad 7... Vyřešte následující soustavu rovnic metodou sčítání:
Uveďme obě rovnice do normálního tvaru. Zde je vhodné použít pravidlo proporce v obou rovnicích. Pokud je v první rovnici pravá strana reprezentována jako a pravá strana druhé rovnice jako, pak bude mít systém tvar:
Máme poměr. Vynásobme její extrémní a střední pojmy. Poté bude mít systém podobu:
První rovnici vynásobíme −3 a ve druhé rozšíříme závorky:
Nyní sečteme obě rovnice. V důsledku sečtení těchto rovnic dostaneme rovnost, v jejíchž obou částech bude nula:
Ukazuje se, že systém má nespočet řešení.
Ale nemůžeme si jen tak vzít z nebe své libovolné hodnoty X a y... Můžeme zadat jednu z hodnot a druhá bude určena v závislosti na hodnotě, kterou jsme zadali. Například ať X= 2. Dosadíme tuto hodnotu do systému:
Výsledkem řešení jedné z rovnic je hodnota pro y což splní obě rovnice:
Výsledná dvojice hodnot (2; −2) uspokojí systém:
Pojďme najít další pár hodnot. Nech být X= 4. Dosaďte do systému tuto hodnotu:
Okem můžete určit, že hodnota y se rovná nule. Pak dostaneme dvojici hodnot (4; 0), která vyhovuje našemu systému:
Příklad 8... Vyřešte následující soustavu rovnic metodou sčítání:
Vynásobte první rovnici 6 a druhou 12
Přepišme, co zbylo:
Vynásobte první rovnici −1. Poté bude mít systém podobu:
Nyní sečteme obě rovnice. V důsledku sčítání vznikne rovnice 6 b= 48, jehož kořen je 8. Dosaz b do první rovnice a najděte A
Systém lineárních rovnic ve třech proměnných
Lineární rovnice se třemi proměnnými obsahuje tři proměnné s koeficienty a také průsečík. Ve své kanonické podobě to může být zapsáno takto:
ax + by + cz = d
Tato rovnice má nespočet řešení. Přidělením dvou proměnných různého významu lze nalézt třetí význam. Řešením je v tomto případě trojnásobek hodnot ( X; y; z), který změní rovnici na identitu.
Pokud proměnné x, y, z jsou spojeny třemi rovnicemi, pak vzniká soustava tří lineárních rovnic se třemi proměnnými. Chcete-li takový systém vyřešit, můžete použít stejné metody, které jsou aplikovány na lineární rovnice se dvěma proměnnými: substituční metoda a metoda sčítání.
Příklad 1... Vyřešte následující soustavu rovnic substituční metodou:
Vyjádřeme se ve třetí rovnici X... Poté bude mít systém podobu:
Nyní provedeme substituci. Variabilní X rovnající se výrazu 3 − 2y − 2z ... Dosaďte tento výraz v první a druhé rovnici:
Otevřeme závorky v obou rovnicích a dáme podobné pojmy:
Došli jsme k systému lineárních rovnic ve dvou proměnných. V tomto případě je vhodné použít metodu sčítání. V důsledku toho proměnná y zmizí a můžeme najít hodnotu proměnné z
Nyní najdeme hodnotu y... K tomu je vhodné použít rovnici - y+ z= 4. Dosaďte do něj hodnotu z
Nyní najdeme hodnotu X... K tomu je vhodné použít rovnici X= 3 − 2y − 2z ... Dosadíme v něm hodnoty y a z
Trojice hodnot (3; −2; 2) je tedy řešením našeho systému. Kontrolou se ujistíme, že tyto hodnoty vyhovují systému:
Příklad 2... Soustavu řešte sčítací metodou
Přidejte první rovnici k druhé vynásobené −2.
Pokud je druhá rovnice vynásobena −2, pak má tvar −6X+ 6y - 4z = −4 ... Nyní to přidejte do první rovnice:
Vidíme, že v důsledku elementárních transformací byla určena hodnota proměnné X... Rovná se jedné.
Vraťme se k hlavnímu systému. Přidejte druhou rovnici ke třetí vynásobené −1. Je-li třetí rovnice vynásobena −1, pak má tvar −4X + 5y − 2z = −1 ... Nyní to přidejte do druhé rovnice:
Dostali jsme rovnici X - 2y= -1. Dosadíme v něm hodnotu X které jsme našli dříve. Potom můžeme určit hodnotu y
Nyní známe hodnoty X a y... To vám umožní určit hodnotu z... Použijme jednu z rovnic obsažených v systému:
Trojice hodnot (1; 1; 1) je tedy řešením našeho systému. Kontrolou se ujistíme, že tyto hodnoty vyhovují systému:
Úlohy pro skládání soustav lineárních rovnic
Problém skládání soustav rovnic je řešen zadáním několika proměnných. Dále jsou na základě podmínek úlohy sestaveny rovnice. Z rovnic sestaví soustavu a vyřeší ji. Po vyřešení systému je nutné zkontrolovat, zda jeho řešení splňuje podmínky problému.
Problém 1... Z města odjelo do JZD auto Volha. Zpět se vracela po jiné silnici, která byla o 5 km kratší než ta první. Celkem auto ujelo 35 km v obou směrech. Kolik kilometrů má každá cesta?
Řešení
Nech být X - délka první cesty, y- délka druhého. Pokud auto ujelo 35 km na oba konce, pak lze první rovnici napsat jako X+ y= 35. Tato rovnice popisuje součet délek obou cest.
Auto se prý vrátilo zpět po silnici, která byla o 5 km kratší než ta první. Pak lze druhou rovnici zapsat jako X− y= 5. Tato rovnice ukazuje, že rozdíl mezi délkami silnic je 5 km.
Nebo lze druhou rovnici napsat jako X= y+ 5. Použijeme tuto rovnici.
Vzhledem k tomu, proměnné X a y v obou rovnicích označují stejné číslo, pak z nich můžeme sestavit systém:
Pojďme tento systém vyřešit některou z dříve studovaných metod. V tomto případě je vhodné použít substituční metodu, protože ve druhé rovnici proměnná X již vyjádřeno.
Dosaďte druhou rovnici do první a najděte y
Dosaďte nalezenou hodnotu y ve druhé rovnici X= y+ 5 a najít X
Délka první cesty byla označena proměnnou X... Nyní jsme našli jeho význam. Variabilní X rovná se 20. Délka první silnice je tedy 20 km.
A délka druhé cesty byla označena y... Hodnota této proměnné je 15. Délka druhé cesty je tedy 15 km.
Pojďme zkontrolovat. Nejprve se ujistěte, že je systém správně vyřešen:
Nyní zkontrolujme, zda řešení (20; 15) splňuje podmínky úlohy.
Auto prý ujelo celkem 35 km v obou směrech. Sečteme délky obou cest a ujistíme se, že řešení (20; 15) splňuje tuto podmínku: 20 km + 15 km = 35 km
Další podmínka: zpět se auto vracelo po jiné silnici, která byla o 5 km kratší než ta první ... Vidíme, že řešení (20; 15) také splňuje tuto podmínku, protože 15 km je kratší než 20 km o 5 km: 20 km - 15 km = 5 km
Při sestavování systému je důležité, aby proměnné označovaly stejná čísla ve všech rovnicích obsažených v tomto systému.
Náš systém tedy obsahuje dvě rovnice. Tyto rovnice zase obsahují proměnné X a y, které představují v obou rovnicích stejná čísla, a to délky silnic rovné 20 km a 15 km.
Úkol 2... Na plošinu byly naloženy dubové a borovicové pražce, celkem 300 ks. Je známo, že všechny dubové pražce vážily o 1 tunu méně než všechny borové pražce. Určete, kolik bylo zvlášť dubových a borových pražců, jestliže každý dubový pražec vážil 46 kg a každý borový pražec 28 kg.
Řešení
Nech být X dub a y na plošinu byly naloženy borové pražce. Pokud by bylo celkem 300 pražců, pak lze první rovnici napsat jako x + y = 300 .
Všechny dubové pražce vážily 46 X kg a borovice vážila 28 y kg. Protože dubové pražce vážily o 1 tunu méně než borové, lze druhou rovnici zapsat jako 28y - 46X= 1000 ... Tato rovnice ukazuje, že rozdíl v hmotnosti mezi dubovými a borovicovými pražci je 1000 kg.
Tuny byly převedeny na kilogramy, protože hmotnost dubových a borových pražců se měří v kilogramech.
Výsledkem jsou dvě rovnice, které tvoří systém
Pojďme vyřešit tento systém. Vyjádřeme se v první rovnici X... Poté bude mít systém podobu:
Dosaďte první rovnici druhou a najděte y
Náhradní y do rovnice X= 300 − y a zjistit, co se rovná X
To znamená, že na plošinu bylo naloženo 100 dubových a 200 borových pražců.
Zkontrolujme, zda řešení (100; 200) splňuje podmínky úlohy. Nejprve se ujistěte, že je systém správně vyřešen:
Celkem prý bylo 300 pražců. Sečtěte počet dubových a borovicových pražců a ujistěte se, že řešení (100; 200) splňuje tuto podmínku: 100 + 200 = 300.
Další podmínka: všechny dubové pražce vážily o 1 tunu méně než všechny borové pražce ... Vidíme, že řešení (100; 200) také splňuje tuto podmínku, protože 46 × 100 kg dubových pražců je lehčích než 28 × 200 kg borových pražců: 5600 kg - 4600 kg = 1000 kg.
Problém 3... Byly odebrány tři kusy slitiny mědi a niklu v hmotnostních poměrech 2:1, 3:1 a 5:1. Vytavil se z nich kus o hmotnosti 12 kg s poměrem mědi a niklu 4:1. Najděte hmotnost každého původního kusu, pokud je hmotnost prvního dvojnásobkem hmotnosti druhého.
Soustavy lineárních rovnic. Přednáška 6.
Soustavy lineárních rovnic.
Základní pojmy.
Zobrazit systém
volala soustava - lineární rovnice s neznámými.
Volají se čísla,, systémové koeficienty.
Čísla se volají volné členy systému, – systémové proměnné... Matice
volala hlavní matrice systému a matrice
– maticový rozšířený systém... Matice - sloupce
A odpovídajícím způsobem matice volných členů a neznámých systému... Potom v maticové formě může být systém rovnic zapsán ve tvaru. Systémové řešení se nazývá hodnoty proměnných, když se dosadí, všechny rovnice systému se změní na skutečné číselné rovnosti. Jakékoli řešení systému může být reprezentováno ve formě matice - sloupce. Pak platí maticová rovnost.
Systém rovnic se nazývá kloub pokud má alespoň jedno řešení a nekonzistentní pokud nemá řešení.
Řešit soustavu lineárních rovnic znamená zjistit, zda je kompatibilní, a v případě kompatibility najít její obecné řešení.
Systém se nazývá homogenní pokud jsou všechny jeho volné členy rovny nule. Homogenní systém je vždy kompatibilní, protože má řešení
Kroneckerova - Copelliho věta.
Odpověď na otázku existence řešení lineárních soustav a jejich jednoznačnosti nám umožňuje získat následující výsledek, který lze formulovat ve formě následujících tvrzení týkajících se soustavy lineárních rovnic s neznámými
(1)
Věta 2... Systém lineárních rovnic (1) je konzistentní tehdy a pouze tehdy, když se hodnost hlavní matice rovná hodnosti rozšířené (.
Věta 3... Pokud je hodnost hlavní matice sdruženého systému lineárních rovnic rovna počtu neznámých, pak má systém jedinečné řešení.
Věta 4... Pokud je hodnost hlavní matice kompatibilního systému menší než počet neznámých, pak má systém nekonečnou množinu řešení.
Pravidla systémového řešení.
3. Najděte vyjádření hlavních proměnných z hlediska volných a získejte obecné řešení soustavy.
4. Zadáním libovolných hodnot volným proměnným se získají všechny hodnoty hlavních proměnných.
Metody řešení soustav lineárních rovnic.
Metoda inverzní matice.
navíc to znamená, že systém má unikátní řešení. Zapišme systém v maticovém tvaru
kde 
,
,
.
Obě strany maticové rovnice vlevo vynásobíme maticí
Od, pak dostaneme, odkud získáme rovnost pro hledání neznámých
Příklad 27. Metodou inverzní matice řešte soustavu lineárních rovnic 
Řešení. Označme hlavní maticí systému
.
Nechť, pak najdeme řešení podle vzorce.
Pojďme počítat.
Od té doby má systém jedinečné řešení. Najděte všechny algebraické doplňky
,
,
,
,
,
,
,
,
Tím pádem
.
Pojďme zkontrolovat
.
Inverzní matice byla nalezena správně. Odtud pomocí vzorce najdeme matici proměnných.
.
Porovnáním hodnot matic dostaneme odpověď:.
Cramerova metoda.
Nechť je dána soustava lineárních rovnic s neznámými
navíc to znamená, že systém má jedinečné řešení. Zapišme řešení soustavy v maticovém tvaru popř
Označujeme
. . . . . . . . . . . . . . ,
Získáme tak vzorce pro nalezení hodnot neznámých, které se nazývají Cramerovy vzorce.
Příklad 28. Vyřešte následující soustavu lineárních rovnic Cramerovou metodou 
.
Řešení. Najdeme determinant hlavní matice systému
.
Od té doby má systém jediné řešení.
Pojďme najít zbývající determinanty pro Cramerovy vzorce
,
,
.
Pomocí Cramerových vzorců najdeme hodnoty proměnných
Gaussova metoda.
Metoda spočívá v sekvenční eliminaci proměnných.
Nechť je dána soustava lineárních rovnic s neznámými.
Gaussův proces řešení se skládá ze dvou fází:
V první fázi je rozšířená matice systému redukována pomocí elementárních transformací do stupňovité formy
,
kde, kterému systém odpovídá
Poté proměnné 
jsou považovány za volné a v každé rovnici jsou přeneseny na pravou stranu.
Ve druhé fázi se z poslední rovnice vyjádří proměnná, výsledná hodnota se dosadí do rovnice. Z této rovnice
je vyjádřena proměnná. Tento proces pokračuje až do první rovnice. Výsledkem je vyjádření hlavních proměnných pomocí volných proměnných 
.
Příklad 29. Vyřešte následující soustavu pomocí Gaussovy metody
Řešení. Vypišme rozšířenou matici soustavy a zredukujme ji do stupňovitého tvaru
.
Protože 
více než počet neznámých, pak je systém konzistentní a má nekonečnou množinu řešení. Napišme systém pro stupňovitou matici
Determinant rozšířené matice tohoto systému, složené z prvních tří sloupců, není roven nule, proto je považován za základní. Proměnné
Budou základní a variabilní bude zdarma. Přeneseme jej ve všech rovnicích na levou stranu
Z poslední rovnice vyjádříme
Dosazením této hodnoty do předposlední druhé rovnice dostaneme
kde 
... Dosazením hodnot proměnných a do první rovnice najdeme 
... Odpověď zapisujeme v následujícím tvaru
- Systémy m lineární rovnice s n neznámý.
Řešení soustavy lineárních rovnic Je taková množina čísel ( x 1, x 2, ..., x n), při dosazení do každé z rovnic systému se získá správná rovnost.
kde a ij, i = 1, ..., m; j = 1,…, n- systémové koeficienty;
b i, i = 1, ..., m- volní členové;
x j, j = 1, ..., n- neznámý.
Výše uvedený systém lze zapsat v maticové formě: A X = B,
kde ( A|B) Je hlavní maticí systému;
A- rozšířená matice systému;
X- sloupec neznámých;
B- sloupec volných členů.
Pokud matice B není nulová matice ∅, pak se tento systém lineárních rovnic nazývá nehomogenní.
Pokud matice B= ∅, pak se tato soustava lineárních rovnic nazývá homogenní. Homogenní systém má vždy nulové (triviální) řešení: x 1 = x 2 =…, x n = 0.
Společná soustava lineárních rovnic Je soustava lineárních rovnic, která má řešení.
Nekonzistentní systém lineárních rovnic Je to soustava lineárních rovnic, která nemá řešení.
Definitivní systém lineárních rovnic Je to systém lineárních rovnic, který má jedinečné řešení.
Neurčitý systém lineárních rovnic Je soustava lineárních rovnic, která má nekonečnou množinu řešení. - Soustavy n lineárních rovnic s n neznámými
Pokud je počet neznámých roven počtu rovnic, pak je matice čtvercová. Determinant matice se nazývá hlavní determinant soustavy lineárních rovnic a označuje se symbolem Δ.
Cramerova metoda k řešení systémů n lineární rovnice s n neznámý.
Cramerovo pravidlo.
Pokud se hlavní determinant soustavy lineárních rovnic nerovná nule, pak je soustava konzistentní a definovaná a jediné řešení se vypočítá podle Cramerových vzorců:
kde Δ i - determinanty získané z hlavního determinantu systému Δ nahrazením i sloupec za volný sloupec členů. ... - Soustavy m lineárních rovnic s n neznámými
Kroneckerova - Capelliho věta.
Aby byl daný systém lineárních rovnic konzistentní, je nutné a postačující, aby hodnost matice systému byla rovna hodnosti rozšířené matice systému, zvonil (Α) = zvonil (Α | B).
Li zvonil (Α) ≠ zvonil (Α | B), pak systém jistě nemá řešení.
Li zvonil (Α) = zvonil (Α | B), pak jsou možné dva případy:
1) zvonil (Α) = n(k počtu neznámých) - řešení je jedinečné a lze jej získat pomocí Cramerových vzorců;
2) zvonil (Α)< n - řešení je nekonečně mnoho. - Gaussova metoda pro řešení soustav lineárních rovnic
Pojďme sestavit rozšířenou matici ( A|B) daného systému koeficientů na neznámé a pravé straně.
Gaussova metoda neboli metoda eliminace neznámých spočívá v redukci rozšířené matice ( A|B) pomocí elementárních transformací přes jeho řady do diagonálního tvaru (do horního trojúhelníkového tvaru). Vrátíme-li se k soustavě rovnic, jsou určeny všechny neznámé.
Mezi elementární transformace přes řetězce patří následující:
1) prohození dvou linek;
2) násobení řetězce číslem jiným než 0;
3) přidání dalšího řetězce vynásobeného libovolným číslem;
4) vyhození nulového řetězce.
Rozšířená matice zmenšená na diagonální tvar odpovídá lineárnímu systému ekvivalentnímu danému, jehož řešení nezpůsobuje potíže. ... - Systém homogenních lineárních rovnic.
Homogenní systém vypadá takto:
odpovídá maticové rovnici A X = 0.
1) Homogenní systém je vždy kompatibilní, protože r (A) = r (A | B), vždy existuje nulové řešení (0, 0,…, 0).
2) Aby měl homogenní systém nenulové řešení, je to nutné a dostatečné r = r (A)< n , což je ekvivalentní Δ = 0.
3) Pokud r< n , pak schválně Δ = 0, pak vznikají volné neznámé c 1, c 2, ..., c n-r, systém má netriviální řešení a je jich nekonečně mnoho.
4) Obecné řešení X na r< n lze zapsat v maticové formě takto:
X = c 1 X 1 + c 2 X 2 +… + c n-r X n-r,
kde jsou řešení X 1, X 2, ..., X n-r tvoří základní systém rozhodování.
5) Základní soustavu řešení lze získat z obecného řešení homogenní soustavy:
,
pokud se postupně předpokládá, že hodnoty parametrů jsou (1, 0,…, 0), (0, 1,…, 0),…, (0, 0,…, 1).
Dekompozice obecného řešení z hlediska fundamentálního systému řešení Je záznamem obecného řešení ve formě lineární kombinace řešení patřících do základního systému.
Teorém... Aby systém lineárních homogenních rovnic měl nenulové řešení, je nutné a postačující, aby Δ ≠ 0.
Pokud je tedy determinant Δ ≠ 0, pak má systém jedinečné řešení.
Je-li Δ ≠ 0, pak má soustava lineárních homogenních rovnic nekonečnou množinu řešení.
Teorém... Aby měl homogenní systém nenulové řešení, je to nutné a dostačující r (A)< n .
Důkaz:
1) r nemůže být víc n(hodnost matice nepřesahuje počet sloupců nebo řádků);
2) r< n od té doby -li r = n, pak hlavním determinantem systému je Δ ≠ 0 a podle Cramerových vzorců existuje jedinečné triviální řešení x 1 = x 2 =… = x n = 0, což odporuje podmínce. Prostředek, r (A)< n .
Následek... Aby byl systém homogenní n lineární rovnice s n neznámé má nenulové řešení, je nutné a postačující, aby Δ = 0.
Řešení soustav lineárních algebraických rovnic (SLAE) je bezpochyby nejdůležitějším tématem kurzu lineární algebry. Obrovské množství úloh ze všech odvětví matematiky je redukováno na řešení soustav lineárních rovnic. Tyto faktory vysvětlují důvod vytvoření tohoto článku. Materiál článku je vybrán a strukturován tak, abyste s jeho pomocí mohli
- zvolit optimální metodu pro řešení vašeho systému lineárních algebraických rovnic,
- studovat teorii zvolené metody,
- vyřešte svůj systém lineárních rovnic podrobným zvážením analyzovaných řešení typických příkladů a problémů.
Stručný popis materiálu článku.
Nejprve uvedeme všechny potřebné definice a pojmy a zavedeme notaci.
Dále se budeme zabývat metodami řešení soustav lineárních algebraických rovnic, ve kterých je počet rovnic roven počtu neznámých proměnných a které mají jednoznačné řešení. Za prvé se zastavme u Cramerovy metody, za druhé si ukažme maticovou metodu řešení takových soustav rovnic a za třetí analyzujme Gaussovu metodu (metodu postupné eliminace neznámých proměnných). Pro upevnění teorie určitě vyřešíme několik SLAE různými způsoby.
Poté přejdeme k řešení soustav lineárních algebraických rovnic obecného tvaru, ve kterých se počet rovnic neshoduje s počtem neznámých proměnných nebo je hlavní matice soustavy degenerovaná. Pojďme formulovat Kroneckerovu - Capelliho větu, která nám umožňuje stanovit kompatibilitu SLAE. Analyzujme řešení systémů (v případě jejich kompatibility) pomocí konceptu základního moll matice. Zvážíme také Gaussovu metodu a podrobně popíšeme řešení příkladů.
Určitě se zastavíme u struktury obecného řešení homogenních a nehomogenních soustav lineárních algebraických rovnic. Uveďme koncept fundamentálního systému řešení a ukažme, jak se obecné řešení SLAE zapisuje pomocí vektorů fundamentálního systému řešení. Pro lepší pochopení se podívejme na pár příkladů.
Na závěr uvažujeme soustavy rovnic, které se redukují na lineární, a také různé problémy, při jejichž řešení vznikají SLAE.
Navigace na stránce.
Definice, pojmy, označení.
Budeme uvažovat soustavy p lineárních algebraických rovnic s n neznámými proměnnými (p se může rovnat n) tvaru
Neznámé proměnné, - koeficienty (některá reálná nebo komplexní čísla), - volné členy (také reálná nebo komplexní čísla).
Tato forma zápisu SLAE se nazývá koordinovat.
PROTI matricový formulář tento systém rovnic má tvar,
kde 
- hlavní matice systému, - matice-sloupec neznámých proměnných, - matice-sloupec volných členů.
Pokud k matici A přidáme jako (n + 1) sloupec matici-sloupec volných členů, dostaneme tzv. rozšířená matrice soustav lineárních rovnic. Obvykle je rozšířená matice označena písmenem T a sloupec volných členů je oddělen svislou čarou od zbytku sloupců, tj. 
Řešením soustavy lineárních algebraických rovnic je sada hodnot neznámých proměnných, která převádí všechny rovnice systému na identity. Maticová rovnice pro dané hodnoty neznámých proměnných se také změní v identitu.
Pokud má soustava rovnic alespoň jedno řešení, pak se nazývá kloub.
Pokud soustava rovnic nemá řešení, pak se nazývá nekonzistentní.
Pokud má SLAE jedinečné řešení, pak se nazývá určitý; pokud existuje více než jedno řešení, pak - nedefinováno.
Jsou-li volné členy všech rovnic soustavy rovny nule 
, pak je zavolán systém homogenní, v opačném případě - heterogenní.
Řešení elementárních soustav lineárních algebraických rovnic.
Pokud je počet rovnic systému roven počtu neznámých proměnných a determinant jeho základní matice není roven nule, pak se takové SLAE budou nazývat základní... Takové soustavy rovnic mají jedinečné řešení a v případě homogenní soustavy jsou všechny neznámé proměnné rovny nule.
Takové SLAU jsme začali studovat na střední škole. Při jejich řešení jsme vzali jednu rovnici, vyjádřili jednu neznámou proměnnou jinými a dosadili ji do zbývajících rovnic, pak jsme vzali další rovnici, vyjádřili další neznámou proměnnou a dosadili ji do jiných rovnic a tak dále. Nebo použili metodu sčítání, to znamená, že přidali dvě nebo více rovnic, aby odstranili nějaké neznámé proměnné. Těmito metodami se nebudeme podrobně zabývat, protože jsou ve skutečnosti modifikacemi Gaussovy metody.
Hlavními metodami řešení elementárních soustav lineárních rovnic jsou Cramerova metoda, maticová metoda a Gaussova metoda. Pojďme je analyzovat.
Řešení soustav lineárních rovnic Cramerovou metodou.
Předpokládejme, že potřebujeme vyřešit soustavu lineárních algebraických rovnic 
ve kterém je počet rovnic roven počtu neznámých proměnných a determinant hlavní matice systému je nenulový, tzn.
Nechť je determinant hlavní matice systému a 
- determinanty matic, které se získají z A nahrazením 1., 2., ..., n sloupec, respektive do sloupce volných členů: 
S tímto zápisem se neznámé proměnné počítají pomocí vzorců Cramerovy metody as 
... Tak se nalézá řešení soustavy lineárních algebraických rovnic Cramerovou metodou.
Příklad.
Cramerova metoda 
.
Řešení.
Hlavní matice systému má tvar 
... Vypočítejme jeho determinant (pokud je to nutné, viz článek): 
Protože determinant hlavní matice systému je nenulový, má systém jedinečné řešení, které lze nalézt Cramerovou metodou.
Pojďme sestavit a vypočítat potřebné determinanty 
(determinant se získá nahrazením prvního sloupce v matici A sloupcem volných členů, determinant - nahrazením druhého sloupce sloupcem volných členů, - nahrazením třetího sloupce matice A sloupcem volných členů ): 
Najděte neznámé proměnné podle vzorců 
:
Odpovědět:
Hlavní nevýhodou Cramerovy metody (pokud ji lze nazvat nevýhodou) je složitost výpočtu determinantů, když je počet rovnic v systému větší než tři.
Řešení soustav lineárních algebraických rovnic maticovou metodou (pomocí inverzní matice).
Nechť je soustava lineárních algebraických rovnic uvedena v maticovém tvaru, kde matice A má rozměr n x n a její determinant je nenulový.
Protože matice A je invertibilní, to znamená, že existuje inverzní matice. Pokud obě strany rovnosti vynásobíme levou, dostaneme vzorec pro nalezení sloupcové matice neznámých proměnných. Dostali jsme tedy řešení soustavy lineárních algebraických rovnic maticovou metodou.
Příklad.
Řešte soustavu lineárních rovnic maticová metoda.
Řešení.
Přepišme soustavu rovnic do maticového tvaru: 
Protože
pak lze SLAE řešit maticovou metodou. Pomocí inverzní matice lze najít řešení tohoto systému jako 
.
Sestrojme inverzní matici pomocí matice algebraických doplňků prvků matice A (pokud je to nutné, viz článek): 
Zbývá vypočítat - matici neznámých proměnných vynásobením inverzní matice 
do sloupcové matice volných členů (v případě potřeby viz článek): 
Odpovědět:
nebo v jiném zápisu x 1 = 4, x 2 = 0, x 3 = -1.
Hlavním problémem při hledání řešení soustav lineárních algebraických rovnic maticovou metodou je složitost hledání inverzní matice, zejména pro čtvercové matice vyššího než třetího řádu.
Řešení soustav lineárních rovnic Gaussovou metodou.
Předpokládejme, že potřebujeme najít řešení systému n lineárních rovnic s n neznámými proměnnými 
determinant hlavní matice je nenulový.
Podstata Gaussovy metody spočívá v postupné eliminaci neznámých proměnných: nejprve je x 1 vyloučeno ze všech rovnic systému, počínaje druhou, pak je x 2 vyloučeno ze všech rovnic, počínaje třetí, a tak dále, dokud pouze neznámá proměnná xn zůstává v poslední rovnici. Takový proces transformace rovnic systému pro postupnou eliminaci neznámých proměnných se nazývá přímým průběhem Gaussovy metody... Po dokončení dopředného běhu Gaussovy metody se z poslední rovnice zjistí x n, pomocí této hodnoty se z předposlední rovnice vypočítá x n-1 a tak dále, z první rovnice se zjistí x 1. Proces výpočtu neznámých proměnných při přechodu od poslední rovnice systému k první se nazývá zpětná Gaussova metoda.
Pojďme si stručně popsat algoritmus pro eliminaci neznámých proměnných.
Budeme předpokládat, že toho můžeme vždy dosáhnout přeskupením rovnic systému. Odstraňte neznámou proměnnou x 1 ze všech rovnic soustavy, počínaje druhou. Abychom to udělali, ke druhé rovnici soustavy přidáme první, vynásobenou, ke třetí rovnici přidáme první, vynásobenou a tak dále, k n-té rovnici přidáme první, vynásobenou. Systém rovnic po takových transformacích nabývá tvaru 
kde a 
.
Ke stejnému výsledku bychom došli, kdybychom x 1 vyjádřili pomocí jiných neznámých proměnných v první rovnici soustavy a výsledný výraz dosadili do všech ostatních rovnic. Proměnná x 1 je tedy vyloučena ze všech rovnic, počínaje druhou.
Dále postupujeme podobným způsobem, ale pouze s částí výsledného systému, který je vyznačen na obrázku 
Abychom to udělali, ke třetí rovnici soustavy přidáme druhou vynásobenou, ke čtvrté rovnici přidáme druhou vynásobenou a tak dále, k n-té rovnici přidáme druhou vynásobenou. Systém rovnic po takových transformacích nabývá tvaru 
kde a 
... Proměnná x 2 je tedy vyloučena ze všech rovnic, počínaje třetí.
Dále přistoupíme k eliminaci neznámé x 3, přičemž obdobně postupujeme s částí soustavy vyznačenou na obr. 
Pokračujeme tedy v přímém průběhu Gaussovy metody, dokud systém nezíská formu 
Od tohoto okamžiku začínáme obrácený průběh Gaussovy metody: z poslední rovnice vypočítáme xn tak, že pomocí získané hodnoty xn zjistíme x n-1 z předposlední rovnice a tak dále, zjistíme x 1 z první rovnice.
Příklad.
Řešte soustavu lineárních rovnic Gaussovou metodou.
Řešení.
Odstraňte neznámou proměnnou x 1 z druhé a třetí rovnice soustavy. Chcete-li to provést, přidejte k oběma částem druhé a třetí rovnice odpovídající části první rovnice, vynásobené respektive: 
Nyní vyloučíme x 2 ze třetí rovnice tím, že k její levé a pravé straně přidáme levou a pravou stranu druhé rovnice, vynásobíme: 
Tím je dopředný pohyb Gaussovy metody dokončen, začínáme zpětný pohyb.
Z poslední rovnice výsledné soustavy rovnic zjistíme x 3: 
Z druhé rovnice dostaneme.
Z první rovnice najdeme zbývající neznámou proměnnou a tím je dokončen opačný průběh Gaussovy metody.
Odpovědět:
Xi = 4, x 2 = 0, x 3 = -1.
Řešení soustav lineárních algebraických rovnic obecného tvaru.
V obecném případě se počet rovnic v systému p neshoduje s počtem neznámých proměnných n:
Takové SLAE nemusí mít žádná řešení, mít jediné řešení nebo mít nekonečně mnoho řešení. Toto tvrzení platí i pro soustavy rovnic, jejichž základní matice je čtvercová a degenerovaná.
Kroneckerova - Capelliho věta.
Před nalezením řešení soustavy lineárních rovnic je nutné zjistit její kompatibilitu. Odpověď na otázku, kdy je SLAE kompatibilní a kdy nekompatibilní, dává Kroneckerova - Capelliho věta:
aby soustava p rovnic s n neznámými (p se může rovnat n) byla konzistentní, je nutné a postačující, aby hodnost hlavní matice systému byla rovna hodnosti rozšířené matice, tj. (A) = pořadí (T).
Uvažujme na příkladu použití Kroneckerovy - Capelliho věty k určení kompatibility soustavy lineárních rovnic.
Příklad.
Zjistěte, zda soustava lineárních rovnic 
řešení.
Řešení.
... Použijme metodu ohraničení nezletilých. Minor druhého řádu 
nenulová. Pojďme vyřešit nezletilé třetího řádu, které s tím sousedí: 
Protože všechny hraničící nezletilé třetího řádu jsou rovny nule, hodnost hlavní matice se rovná dvěma.
Na druhé straně hodnost rozšířené matice 
je roven třem, protože třetí řád moll 
nenulová.
Tím pádem, Rang (A), tedy Kroneckerovou - Capelliho větou, můžeme dojít k závěru, že původní systém lineárních rovnic je nekonzistentní.
Odpovědět:
Systém nemá řešení.
Naučili jsme se tedy stanovit nekonzistenci systému pomocí Kroneckerovy - Capelliho věty.
Jak ale najít řešení pro SLAE, pokud byla prokázána jeho kompatibilita?
K tomu potřebujeme koncept základního moll matice a větu o hodnosti matice.
Zavolá se menší nejvyšší řád matice A, jiný než nula základní.
Z definice základního minoru vyplývá, že jeho pořadí se rovná hodnosti matice. Pro nenulovou matici A může být několik základních mollů, vždy je jeden základní moll.
Vezměme si například matici 
.
Všechny minoritní hodnoty třetího řádu této matice jsou rovny nule, protože prvky třetího řádku této matice jsou součtem odpovídajících prvků prvního a druhého řádku.
Následující nezletilí druhého řádu jsou základní, protože jsou nenulové 
Nezletilí 
nejsou základní, protože se rovnají nule.
Věta o hodnosti matice.
Pokud je hodnost matice řádu p x n rovna r, pak všechny prvky řádků (a sloupců) matice, které netvoří vybranou základní mollovou, jsou lineárně vyjádřeny pomocí odpovídajících prvků řádků ( a sloupce), které tvoří základní moll.
Co nám dává věta o hodnosti matice?
Pokud jsme Kroneckerovou - Capelliho větou stanovili kompatibilitu systému, pak zvolíme libovolnou základní moll základní matice systému (její řád je r) a vyřadíme ze systému všechny rovnice, které netvoří zvolená základní moll. Takto získaný SLAE bude ekvivalentní původnímu, protože vyřazené rovnice jsou stále nadbytečné (podle věty o pořadí matice jsou lineární kombinací zbývajících rovnic).
V důsledku toho jsou po vyřazení nepotřebných rovnic systému možné dva případy.
Pokud je počet rovnic r ve výsledné soustavě roven počtu neznámých proměnných, pak bude definitivní a jediné řešení lze nalézt Cramerovou metodou, maticovou metodou nebo Gaussovou metodou.
Příklad.
.
Řešení.
Hodnost hlavní matice systému 
je roven dvěma, protože druhý řád je menší 
nenulová. Rozšířená hodnost Matrix 
je také roven dvěma, protože jediná minoritní skupina třetího řádu je rovna nule 
a výše zmíněný moll druhého řádu je nenulový. Na základě Kroneckerovy - Capelliho věty můžeme tvrdit kompatibilitu původního systému lineárních rovnic, protože Pořadí (A) = Pořadí (T) = 2.
Bereme jako základní vedlejší ... Je tvořen koeficienty první a druhé rovnice: 
Třetí rovnice soustavy se nepodílí na tvorbě základní moll, proto ji ze soustavy na základě věty o hodnosti matice vyloučíme: 
Tak jsme dostali elementární systém lineárních algebraických rovnic. Pojďme to vyřešit pomocí Cramerovy metody: 
Odpovědět:
x 1 = 1, x 2 = 2.
Pokud je počet rovnic r v získaném SLAE menší než počet neznámých proměnných n, pak v levých stranách rovnic ponecháme členy tvořící základní moll, zbytek členů se přenese do pravého- ruční strany rovnic soustavy s opačným znaménkem.
Volají se neznámé proměnné (je jich r), které zůstávají na levé straně rovnic hlavní.
Neznámé proměnné (existuje n - r kusů), které se objevují na pravé straně, jsou volány volný, uvolnit.
Nyní předpokládáme, že volné neznámé proměnné mohou nabývat libovolných hodnot a r základních neznámých proměnných bude vyjádřeno pomocí volných neznámých proměnných jedinečným způsobem. Jejich vyjádření lze nalézt řešením získaných SLAE Cramerovou metodou, maticovou metodou nebo Gaussovou metodou.
Vezměme si příklad.
Příklad.
Řešte soustavu lineárních algebraických rovnic 
.
Řešení.
Najděte hodnost hlavní matice systému 
metodou ohraničení nezletilých. Vezmeme 1 1 = 1 jako nenulovou minoritní hodnotu prvního řádu. Začněme hledat nenulovou moll druhého řádu, která obklopuje tuto moll: 
Takto jsme našli nenulovou moll 2. řádu. Začněme hledat nenulovou hraniční moll třetího řádu: 
Hodnost hlavní matice je tedy tři. Hodnost rozšířené matice je také tři, to znamená, že systém je konzistentní.
Jako základní bereme nalezený nenulový moll třetího řádu.
Pro názornost uvádíme prvky, které tvoří základní moll: 
Ponecháme na levé straně rovnic soustavy členy, které se účastní základní moll, a zbytek přeneseme s opačnými znaménky na pravé strany: 
Volným neznámým proměnným x 2 a x 5 přiřaďme libovolné hodnoty, tedy vezmeme 
, kde jsou libovolná čísla. V tomto případě bude mít SLAE formu 
Výsledný elementární systém lineárních algebraických rovnic je řešen Cramerovou metodou: 
Proto, .
Nezapomeňte ve své odpovědi uvést volné neznámé proměnné.
Odpovědět:
Kde jsou libovolná čísla.
Shrnout.
Pro řešení soustavy lineárních algebraických rovnic obecného tvaru nejprve zjistíme její kompatibilitu pomocí Kroneckerovy - Capelliho věty. Pokud se hodnost hlavní matice nerovná hodnosti rozšířené matice, docházíme k závěru, že systém je nekompatibilní.
Pokud se hodnost hlavní matice rovná hodnosti rozšířené matice, vybereme základní mollovou a zahodíme rovnice systému, které se nepodílejí na tvorbě vybrané základní vedlejší matice.
Pokud je řád základní moll roven počtu neznámých proměnných, pak má SLAE jedinečné řešení, které najdeme jakoukoliv známou metodou.
Pokud je řád základní moll menší než počet neznámých proměnných, pak na levé straně rovnic soustavy ponecháme členy se základními neznámými proměnnými, zbývající členy přeneseme na pravé strany a zadejte libovolné hodnoty volným neznámým proměnným. Z výsledné soustavy lineárních rovnic najdeme hlavní neznámé proměnné Cramerovou metodou, maticovou metodou nebo Gaussovou metodou.
Gaussova metoda pro řešení soustav lineárních algebraických rovnic obecného tvaru.
Gaussovu metodu lze použít k řešení systémů lineárních algebraických rovnic jakéhokoli druhu, aniž by bylo nutné nejprve zkoumat jejich kompatibilitu. Proces postupné eliminace neznámých proměnných umožňuje usuzovat na kompatibilitu i nekompatibilitu SLAE, a pokud existuje řešení, umožňuje jej najít.
Z hlediska výpočetní práce je výhodnější Gaussova metoda.
Její podrobný popis a analyzované příklady naleznete v článku Gaussova metoda řešení soustav lineárních algebraických rovnic obecného tvaru.
Zápis obecného řešení homogenních a nehomogenních lineárních algebraických systémů pomocí vektorů základního systému řešení.
V této části se zaměříme na kompatibilní homogenní a nehomogenní systémy lineárních algebraických rovnic s nekonečnou množinou řešení.
Pojďme se nejprve zabývat homogenními systémy.
Základní rozhodovací systém Homogenní soustava p lineárních algebraických rovnic s n neznámými proměnnými je množinou (n - r) lineárně nezávislých řešení této soustavy, kde r je řád základní moll základní matice soustavy.
Označíme-li lineárně nezávislá řešení homogenní SLAE jako X (1), X (2),…, X (nr) (X (1), X (2),…, X (nr) je n x 1 sloupcové matice), pak je obecné řešení tohoto homogenního systému reprezentováno jako lineární kombinace vektorů základního systému řešení s libovolnými konstantními koeficienty С 1, С 2, ..., С (nr), tzn.
Co znamená pojem obecné řešení homogenní soustavy lineárních algebraických rovnic (oroslau)?
Význam je jednoduchý: vzorec specifikuje všechna možná řešení původního SLAE, jinými slovy, vezme libovolnou sadu hodnot libovolných konstant С 1, С 2, ..., С (nr), podle vzorce my získat jedno z řešení původního homogenního SLAE.
Pokud tedy najdeme fundamentální systém řešení, pak budeme schopni specifikovat všechna řešení tohoto homogenního SLAE as.
Ukažme si proces konstrukce základního systému řešení homogenního SLAE.
Zvolíme základní moll původní soustavy lineárních rovnic, vyloučíme ze soustavy všechny ostatní rovnice a všechny členy obsahující volné neznámé proměnné přeneseme na pravé strany rovnic soustavy s opačnými znaménky. Volným neznámým proměnným dáme hodnoty 1,0,0, ..., 0 a hlavní neznámé vypočítáme řešením získané elementární soustavy lineárních rovnic libovolným způsobem, například Cramerovou metodou. To dá X (1) - první řešení základního systému. Pokud dáme volným neznámým hodnoty 0,1,0,0,…, 0 a vypočítáme hlavní neznámé, dostaneme X (2). Atd. Pokud volným neznámým proměnným dáme hodnoty 0,0, ..., 0,1 a vypočítáme základní neznámé, dostaneme X (n-r). Takto bude sestaven základní systém řešení homogenního SLAE a jeho obecné řešení lze zapsat do formuláře.
Pro nehomogenní systémy lineárních algebraických rovnic je obecné řešení reprezentováno ve tvaru, kde je obecné řešení odpovídajícího homogenního systému a je partikulárním řešením původního nehomogenního SLAE, které získáme tak, že volným neznámým dáme hodnoty 0,0, ..., 0 a výpočet hodnot hlavních neznámých.
Podívejme se na příklady.
Příklad.
Najděte základní soustavu řešení a obecné řešení homogenní soustavy lineárních algebraických rovnic 
.
Řešení.
Hodnost hlavní matice homogenních soustav lineárních rovnic je vždy rovna hodnosti rozšířené matice. Nalezněme hodnost hlavní matice metodou ohraničení minors. Jako nenulový moll prvního řádu vezmeme prvek a 1 1 = 9 hlavní matice systému. Najděte hraniční nenulovou moll druhého řádu: 
Byl nalezen nenulový minor druhého řádu. Pojďme iterovat přes nezletilé třetího řádu, které s ním sousedí, a hledat nenulovou jedničku: 
Všechny hraniční vedlejší matice třetího řádu jsou rovny nule, proto je hodnost hlavní a rozšířené matice rovna dvěma. Berte jako základní vedlejší. Pro přehlednost si všimneme prvků systému, které jej tvoří: 
Třetí rovnice původního SLAE se nepodílí na tvorbě základní moll, proto ji lze vyloučit: 
Na pravé straně rovnic ponecháme členy obsahující hlavní neznámé a na pravé straně přeneseme členy s volnými neznámými:
Sestavme základní soustavu řešení původní homogenní soustavy lineárních rovnic. Fundamentální systém řešení tohoto SLAE se skládá ze dvou řešení, protože původní SLAE obsahuje čtyři neznámé proměnné a řád jeho základní minor je dvě. Abychom našli X (1), přiřadíme volným neznámým proměnným hodnoty x 2 = 1, x 4 = 0, poté najdeme hlavní neznámé ze soustavy rovnic 
.