Teorie Kramerovy a Gaussovy metody. Kramerova metoda řešení soustav lineárních rovnic

Uvažujme soustavu 3 rovnic se třemi neznámými

Pomocí determinantů třetího řádu lze řešení takové soustavy zapsat ve stejném tvaru jako u soustavy dvou rovnic, tzn.

(2.4)

pokud 0. Tady

to je Cramerovo pravidlo řešení soustavy tří lineárních rovnic o třech neznámých.

Příklad 2.3. Vyřešte soustavu lineárních rovnic pomocí Cramerova pravidla:

Řešení ... Najděte determinant hlavní matice systému

Od 0 můžeme použít Cramerovo pravidlo k nalezení řešení systému, ale nejprve vypočítáme tři další determinanty:

Zkouška:

Proto bylo řešení nalezeno správně. 

Cramerova pravidla získaná pro lineární systémy 2. a 3. řádu naznačují, že stejná pravidla lze formulovat pro lineární systémy libovolného řádu. Opravdu se odehrává

Cramerův teorém. Kvadratická soustava lineárních rovnic s nenulovým determinantem hlavní matice soustavy (0) má jedno a pouze jedno řešení a toto řešení se vypočítá podle vzorců

(2.5)

kde  – determinant hlavní matice,  i – determinant matice, odvozený od hlavního, náhradníhoisloupec sloupcem volných členů.

Všimněte si, že pokud  = 0, pak Cramerovo pravidlo neplatí. To znamená, že systém buď nemá vůbec žádná řešení, nebo má nekonečně mnoho řešení.

Po zformulování Cramerova teorému přirozeně vyvstává otázka výpočtu determinantů vyšších řádů.

2.4. Determinanty n-tého řádu

Další vedlejší M ijživel A ij se nazývá determinant získaný z daného vymazáním iřádek a j sloupec. Algebraický doplněk A ijživel A ij se nazývá moll tohoto prvku, bere se se znaménkem (–1) i + j, tj. A ij = (–1) i + j M ij .

Najděte například nezletilé a doplňky prvků A 23 a A 31 determinantů

Dostaneme



Pomocí konceptu algebraického doplňku můžeme formulovat Věta o determinantním rozkladunpořadí podle řádku nebo sloupce.

Věta 2.1. Determinant maticeAse rovná součtu součinů všech prvků určitého řádku (nebo sloupce) jejich algebraickými doplňky:

(2.6)

Tato věta je základem jedné z hlavních metod pro výpočet determinantů, tzv. způsob redukce objednávky... V důsledku expanze determinantu n-tého řádu v libovolném řádku nebo sloupci, dostaneme n determinantů ( n–1) pořadí. Pro snížení počtu takových determinantů je vhodné vybrat řádek nebo sloupec s největším počtem nul. V praxi se vzorec pro rozšíření determinantu obvykle zapisuje ve tvaru:

těch. algebraické doplňky jsou psány výslovně v termínech minors.

Příklady 2.4. Vypočítejte determinanty tak, že je nejprve rozbalíte do libovolného řádku nebo sloupce. V takových případech obvykle vyberte sloupec nebo řádek s největším počtem nul. Vybraný řádek nebo sloupec bude označen šipkou.



2.5. Základní vlastnosti determinantů

Rozšířením determinantu v libovolném řádku nebo sloupci získáme n determinantů ( n–1) pořadí. Pak každý z těchto determinantů ( n–1) -tý řád lze také rozšířit na součet determinantů ( n–2) pořadí. Pokračováním v tomto procesu lze dosáhnout determinantů 1. řádu, tzn. na prvky matice, jejíž determinant se vypočítá. Pro výpočet determinantů 2. řádu je tedy nutné vypočítat součet dvou členů, pro determinanty 3. řádu součet 6 členů, pro determinanty 4. řádu 24 členů. Počet členů bude prudce narůstat s rostoucím pořadím determinantu. To znamená, že výpočet determinantů velmi vysokých řádů se stává poměrně pracným úkolem, nad síly i počítače. Je však možné vypočítat determinanty i jiným způsobem, pomocí vlastností determinantů.

Nemovitost 1 . Determinant se nezmění, pokud se v něm prohodí řádky a sloupce, tzn. při transponované matici:

.

Tato vlastnost udává rovnost řádků a sloupců determinantu. Jinými slovy, jakékoli tvrzení o sloupcích determinantu platí pro jeho řádky a naopak.

Nemovitost 2 . Při prohození dvou řádků (sloupců) se determinant změní znaménko.

Následek . Pokud má determinant dva stejné řádky (sloupce), pak je roven nule.

Nemovitost 3 . Společný faktor všech prvků v libovolném řádku (sloupci) lze posunout za znaménko determinantu.

Například,

Následek . Pokud jsou všechny prvky některého řádku (sloupce) determinantu rovny nule, pak samotný determinant je roven nule.

Nemovitost 4 . Determinant se nezmění, pokud k prvkům jednoho řádku (sloupce) přidáme prvky jiného řádku (sloupce), vynásobíme nějakým číslem.

Například,

Nemovitost 5 . Determinant maticového součinu se rovná součinu determinantů matic:

Nechť soustava lineárních rovnic obsahuje tolik rovnic, kolik je nezávisle proměnných, tzn. má formu

Takové soustavy lineárních rovnic se nazývají kvadratické. Determinant složený z koeficientů nezávislých proměnných systému (1.5) se nazývá hlavní determinant systému. Budeme jej označovat řeckým písmenem D.

Pokud je hlavní determinant libovolný ( j-tý) sloupec, nahraďte sloupcem volných podmínek systému (1.5), pak můžeme získat další n pomocné determinanty:

(j = 1, 2, …, n). (1.7)

Cramerovo pravidlořešení kvadratických soustav lineárních rovnic je následující. Pokud je hlavní determinant D soustavy (1.5) nenulový, pak má soustava jednoznačné řešení, které lze nalézt pomocí vzorců:

Příklad 1.5. Použití Cramerovy metody k řešení soustavy rovnic

Vypočítejme hlavní determinant systému:

Od D¹0 má systém jedinečné řešení, které lze nalézt pomocí vzorců (1.8):

Tím pádem,

Maticové operace

1. Násobení matice číslem. Operace násobení matice číslem je definována následovně.

2. Abyste mohli matici vynásobit číslem, musíte tímto číslem vynásobit všechny její prvky. To znamená

Příklad 1.6. .

Sčítání matic.

Tato operace je zavedena pouze pro matice stejného řádu.

Aby bylo možné přidat dvě matice, je nutné přidat odpovídající prvky druhé matice k prvkům jedné matice:

(1.10)
Operace sčítání matic má vlastnosti asociativnosti a komutativnosti.

Příklad 1.7. .

Maticové násobení.

Pokud počet sloupců v matici A odpovídá počtu řádků v matici PROTI, pak je pro tyto matice zavedena operace násobení:

Tedy při násobení matice A rozměry m´ n na matrice PROTI rozměry n´ k dostaneme matrici S rozměry m´ k... Navíc prvky matice S se počítají pomocí následujících vzorců:

Úkol 1.8. Najděte, pokud je to možné, součin matic AB a BA:

Řešení. 1) Najít práci AB, potřebujete řádky matice A vynásobte sloupci matice B:

2) Umělecké dílo BA neexistuje, protože počet sloupců v matici B neodpovídá počtu řádků v matici A.

Inverzní matice. Maticové řešení soustav lineárních rovnic

Matice A - 1 se nazývá inverze čtvercové matice A pokud platí rovnost:

kam skrz já označuje matici identity stejného řádu jako matice A:

Aby čtvercová matice měla inverzi, je nutné a postačující, aby její determinant byl nenulový. Inverzní matici najdeme podle vzorce:

kde A ij- algebraické sčítání prvků a ij matrice A(Všimněte si, že algebraické doplňuje řádky matice A jsou umístěny v inverzní matici ve formě odpovídajících sloupců).

Příklad 1.9. Najděte inverzní matici A - 1 do matice

Inverzní matici najdeme vzorcem (1.13), který pro případ n= 3 má tvar:

Najít det A = | A| = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 - 3 × 3 × 3 - 1 × 5 × 4 - 2 × 2 × 8 = 24 + 30 + 24 - 27 - 20 - 32 = - 1. Protože determinant původní matice je nenulový, existuje inverzní matice.

1) Najděte algebraické doplňky A ij:

Pro usnadnění nalezení inverzní matice jsme umístili algebraické doplňky k řádkům původní matice do odpovídajících sloupců.

Ze získaných algebraických doplňků sestavíme novou matici a vydělíme ji determinantem det A... Dostaneme tedy inverzní hodnotu matice:

Kvadratické soustavy lineárních rovnic s nenulovým hlavním determinantem lze řešit pomocí inverzní matice. Za tímto účelem je systém (1.5) napsán v maticovém tvaru:

Vynásobením obou stran rovnosti (1,14) vlevo A - 1, dostaneme řešení soustavy:

Abyste tedy našli řešení čtvercové soustavy, musíte najít inverzní matici k hlavní matici soustavy a vynásobit ji vpravo sloupcovou maticí volných členů.

Úkol 1.10.Řešte soustavu lineárních rovnic

pomocí inverzní matice.

Řešení. Zapišme systém v maticovém tvaru:,

kde je hlavní matice systému, je sloupec neznámých a je sloupec volných členů. Protože hlavní determinant systému, hlavní matice systému A má inverzní matici A-1. Najít inverzní matici A-1, vypočítáme algebraické doplňky ke všem prvkům matice A:

Ze získaných čísel poskládáme matici (navíc algebraické doplňky k řádkům matice A zapíšeme do odpovídajících sloupců) a vydělíme determinantem D. Našli jsme tedy inverzní matici:

Řešení soustavy najdeme podle vzorce (1.15):

Tím pádem,

Řešení soustav lineárních rovnic metodou obyčejných Jordanových výjimek

Nechť je dán libovolný (ne nutně kvadratický) systém lineárních rovnic:

Je potřeba najít řešení systému, tzn. množina proměnných, která splňuje všechny rovnosti systému (1.16). V obecném případě může mít soustava (1.16) nejen jedno řešení, ale i nekonečně mnoho řešení. Také nemusí mít vůbec žádné řešení.

Při řešení takových problémů se používá metoda eliminace neznámých dobře známá ze školního kurzu, které se také říká metoda obyčejných Jordanových výjimek. Podstatou této metody je, že v jedné z rovnic soustavy (1.16) je jedna z proměnných vyjádřena pomocí jiných proměnných. Poté se tato proměnná dosadí do jiných rovnic systému. Výsledkem je systém, který obsahuje o jednu rovnici a proměnnou méně než původní systém. Rovnice, ze které byla proměnná vyjádřena, je zapamatována.

Tento proces se opakuje, dokud v systému nezůstane poslední rovnice. V procesu eliminace neznámých se některé rovnice mohou proměnit například ve skutečné identity. Takové rovnice jsou ze systému vyloučeny, protože jsou splněny pro jakékoli hodnoty proměnných, a proto neovlivňují řešení systému. Pokud se v procesu eliminace neznámých alespoň jedna rovnice stane rovností, která nemůže být splněna pro žádné hodnoty proměnných (například), docházíme k závěru, že systém nemá řešení.

Pokud v průběhu řešení nevznikly žádné protichůdné rovnice, pak se jedna z proměnných v ní zbývajících zjistí z poslední rovnice. Pokud v poslední rovnici zbývá pouze jedna proměnná, pak je vyjádřena jako číslo. Pokud v poslední rovnici zůstanou další proměnné, pak jsou považovány za parametry a proměnná vyjádřená prostřednictvím nich bude funkcí těchto parametrů. Poté dojde k tzv. „reverse move“. Nalezená proměnná je dosazena do poslední zapamatované rovnice a je nalezena druhá proměnná. Poté jsou dvě nalezené proměnné dosazeny do předposlední zapamatované rovnice a je nalezena třetí proměnná a tak dále, až k první zapamatované rovnici.

Výsledkem je řešení systému. Toto řešení bude jediné, pokud jsou nalezené proměnné čísla. Pokud první nalezená proměnná a poté všechny ostatní závisí na parametrech, pak bude mít systém nekonečný počet řešení (každé sadě parametrů odpovídá nové řešení). Vzorce, které umožňují najít řešení systému v závislosti na konkrétní sadě parametrů, se nazývají obecné řešení systému.

Příklad 1.11.

X

Po zapamatování první rovnice a zmenšení podobných členů ve druhé a třetí rovnici se dostaneme k systému:

Pojďme se vyjádřit y z druhé rovnice a dosaďte ji do rovnice první:

Zapamatujme si druhou rovnici a z první najdeme z:

Provedením zpětného pohybu postupně nacházíme y a z... K tomu nejprve dosadíme do poslední zapamatované rovnice, odkud najdeme y:

Pak dosadíme i do první zapamatované rovnice, odkud najdeme X:

Úkol 1.12. Vyřešte soustavu lineárních rovnic eliminací neznámých:

Řešení. Vyjádřeme z první rovnice proměnnou X a dosaďte jej do druhé a třetí rovnice:

V tomto systému si první a druhá rovnice odporují. Opravdu, vyjadřující y z první rovnice a jejím dosazením do druhé rovnice dostaneme, že 14 = 17. Tato rovnost neplatí pro žádné hodnoty proměnných X, y, a z... V důsledku toho je systém (1.17) nekonzistentní, tj. nemá řešení.

Doporučujeme čtenářům, aby si nezávisle ověřili, že hlavní determinant původního systému (1.17) je roven nule.

Uvažujme systém, který se od systému (1.17) liší pouze jedním volným členem.

Úkol 1.13. Vyřešte soustavu lineárních rovnic eliminací neznámých:

Řešení. Stejně jako dříve vyjádříme z první rovnice proměnnou X a dosaďte jej do druhé a třetí rovnice:

Zapamatujme si první rovnici a do druhé a třetí rovnice uveďme podobné členy. Dostáváme se k systému:

Vyjadřování y z první rovnice a jejím dosazením do druhé rovnice získáme identitu 14 = 14, která neovlivňuje řešení soustavy, a proto ji lze ze soustavy vyloučit.

V poslední zapamatované rovnosti proměnná z bude považován za parametr. Věříme. Pak

Náhradní y a z do první zapamatované rovnosti a najít X:

Systém (1.18) má tedy nekonečnou množinu řešení a jakékoli řešení lze nalézt pomocí vzorců (1.19), přičemž zvolíme libovolnou hodnotu parametru t:

(1.19)
Řešením soustavy jsou tedy např. následující množiny proměnných (1; 2; 0), (2; 26; 14) atd. Vzorce (1.19) vyjadřují obecné (libovolné) řešení soustavy (1.18) .

V případě, kdy má původní systém (1.16) dostatečně velký počet rovnic a neznámých, se naznačená metoda obyčejných Jordanových výjimek jeví jako těžkopádná. Nicméně není. Algoritmus pro přepočet koeficientů systému stačí v jednom kroku odvodit v obecné podobě a zformulovat řešení problému ve formě speciálních Jordanových tabulek.

Nechť je dána soustava lineárních forem (rovnic):

, (1.20)
kde x j- nezávislé (hledané) proměnné, a ij- konstantní koeficienty
(i = 1, 2,…, m; j = 1, 2,…, n). Pravá strana systému y i (i = 1, 2,…, m) mohou být jak proměnné (závislé), tak konstanty. Je nutné najít řešení tohoto systému odstraněním neznámých.

Zvažte následující operaci, dále nazývanou „jeden krok běžných jordánských výjimek“. Z libovolného ( r-th) rovnost, vyjadřujeme libovolnou proměnnou ( x s) a nahradit ve všech ostatních rovnoprávnostech. To je samozřejmě možné pouze v případě a rs¹ 0. Koeficient a rs nazývaný povolující (někdy řídící nebo hlavní) prvek.

Získáme následující systém:

Z s rovnosti systému (1.21), následně najdeme proměnnou x s(po nalezení zbytku proměnných). S-tý řádek je zapamatován a dále vyloučen ze systému. Zbývající systém bude obsahovat o jednu rovnici a o jednu nezávislou proměnnou méně než původní systém.

Vypočítejme koeficienty výsledného systému (1.21) z hlediska koeficientů původního systému (1.20). Začněme s r-tá rovnice, která po vyjádření proměnné x s přes zbytek proměnných bude vypadat takto:

Tedy nové koeficienty r-té rovnice se počítají podle následujících vzorců:

(1.23)
Nyní spočítáme nové koeficienty b ij(i¹ r) libovolné rovnice. K tomu dosadíme proměnnou vyjádřenou v (1.22) x s proti i-tá rovnice soustavy (1.20):

Po uvedení podobných podmínek dostaneme:

(1.24)
Z rovnosti (1.24) získáme vzorce, podle kterých se vypočítávají zbývající koeficienty soustavy (1.21) (s výjimkou r rovnice):

(1.25)
Transformace soustav lineárních rovnic metodou obyčejných Jordanových výjimek je formalizována ve formě tabulek (matic). Tyto tabulky se nazývají "Jordánské" tabulky.

Problém (1.20) je tedy spojen s následující Jordanovou tabulkou:

Tabulka 1.1

	X 1	X 2	…	x j	…	x s	…	x n
y 1 =	A 11	A 12		A 1j		A 1s		A 1n
…………………………………………………………………..
y i=	a i 1	a i 2		a ij		a je		v
…………………………………………………………………..
r=	a r 1	a r 2		a rj		a rs		a rn
………………………………………………………………….
y n=	a m 1	a m 2		a mj		paní		a mn

Jordanova tabulka 1.1 obsahuje levý sloupec záhlaví, do kterého jsou zapsány pravé strany systému (1.20), a horní řádek záhlaví, do kterého jsou zapsány nezávislé proměnné.

Zbytek prvků tabulky tvoří hlavní matici koeficientů systému (1.20). Pokud matici vynásobíme A do matice sestávající z prvků horního řádku nadpisu, pak dostanete matici skládající se z prvků levého sloupce nadpisu. To znamená, že Jordanova tabulka je v podstatě maticová forma zápisu systému lineárních rovnic:. Systém (1.21) v tomto případě odpovídá následující Jordan tabulce:

Tabulka 1.2

	X 1	X 2	…	x j	…	r	…	x n
y 1 =	b 11	b 12		b 1 j		b 1 s		b 1 n
…………………………………………………………………..
y i =	b i 1	b i 2		b ij		b je		b v
…………………………………………………………………..
x s =	b r 1	b r 2		b rj		b rs		b rn
………………………………………………………………….
y n =	b m 1	b m 2		b mj		b ms		b mn

Permisivní prvek a rs zvýrazníme to tučně. Připomeňme, že aby se uskutečnil jeden krok Jordanových výjimek, musí být rozlišovací prvek nenulový. Řádek tabulky, který obsahuje povolující prvek, se nazývá povolovací řádek. Sloupec obsahující povolovací prvek se nazývá povolovací sloupec. Při přesunu z této tabulky do další tabulky se jedna proměnná ( x s) z horního řádku záhlaví tabulky se přesune do levého sloupce záhlaví a naopak jeden z volných členů systému ( r) z levého záhlaví tabulky se přesune do horního záhlaví.

Popišme si algoritmus pro přepočet koeficientů při přechodu z Jordanovy tabulky (1.1) do tabulky (1.2), který vyplývá ze vzorců (1.23) a (1.25).

1. Povolovací prvek je nahrazen recipročním:

2. Zbývající prvky povolovací čáry jsou rozděleny povolovacím prvkem a změní se znak na opačný:

3. Zbývající prvky rozlišovacího sloupce jsou rozděleny na rozlišovací prvek:

4. Prvky, které nejsou zahrnuty v rozlišovacím řádku a rozlišovacím sloupci, se přepočítají pomocí vzorců:

Poslední vzorec je snadno zapamatovatelný, pokud si všimnete, že prvky tvořící zlomek jsou v průsečíku ičt a r-té řádky a jčt a s-té sloupce (rozlišovací řádek, rozlišovací sloupec a řádek a sloupec, na jejichž průsečíku se nachází přepočítávaný prvek). Přesněji, při zapamatování vzorce můžete použít následující diagram:

-21 -26 -13 -37

Vezmeme-li první krok Jordanových výjimek, jakýkoli prvek z tabulky 1.3, který se nachází ve sloupcích X 1 ,…, X 5 (všechny uvedené prvky jsou nenulové). Měli byste nejen vybrat rozlišovací prvek v posledním sloupci, protože je potřeba najít nezávislé proměnné X 1 ,…, X 5. Zvolíme např. koeficient 1 s proměnnou X 3 ve třetím řádku tabulky 1.3 (povolovací prvek je zobrazen tučně). Přejděte na tabulku 1.4, proměnná X 3 z horního řádku nadpisu se zamění za konstantu 0 levého hlavového sloupce (třetí řádek). V tomto případě proměnná X 3 je vyjádřena pomocí zbývajících proměnných.

Tětiva X 3 (tabulka 1.4) lze po zapamatování vyloučit z tabulky 1.4. Třetí sloupec s nulou v horním záhlaví je rovněž vyloučen z tabulky 1.4. Faktem je, že bez ohledu na koeficienty tohoto sloupce b i 3 všechny odpovídající členy každé rovnice 0 b i 3 systémy budou nulové. Proto lze tyto koeficienty vynechat. Eliminace jedné proměnné X 3 a zapamatováním jedné z rovnic se dostaneme k soustavě odpovídající tabulce 1.4 (s přeškrtnutou čarou X 3). Výběr v tabulce 1.4 jako rozlišovací prvek b 14 = -5, přejděte k tabulce 1.5. V tabulce 1.5 si pamatujeme první řádek a vyloučíme jej z tabulky spolu se čtvrtým sloupcem (s nulou nahoře).

Tabulka 1.5 Tabulka 1.6

Z poslední tabulky 1.7 najdeme: X 1 = - 3 + 2X 5 .

Postupným dosazením již nalezených proměnných do uložených řádků najdeme zbývající proměnné:

Systém má tedy nespočet řešení. Variabilní X 5, můžete přiřadit libovolné hodnoty. Tato proměnná funguje jako parametr X 5 = t. Prokázali jsme kompatibilitu systému a našli jeho obecné řešení:

X 1 = - 3 + 2t

X 2 = - 1 - 3t

X 3 = - 2 + 4t . (1.27)
X 4 = 4 + 5t

X 5 = t

Uvedením parametru t různých hodnot, získáme nespočet řešení původního systému. Takže například řešením systému je následující sada proměnných (- 3; - 1; - 2; 4; 0).

Nechť je dána soustava tří lineárních rovnic:

Pro řešení soustavy lineárních rovnic Cramerovou metodou je hlavní determinant soustavy  sestaven z koeficientů při neznámých. Pro systém (1) má hlavní determinant tvar
.

Dále jsou pro proměnné sestaveny determinanty
,,... K tomu se v hlavním determinantu místo sloupce koeficientů pro odpovídající proměnnou zapíše sloupec volných členů, tzn.

,
,
.

Pak je řešení soustavy nalezeno pomocí Cramerových vzorců

,
,

Je třeba poznamenat, že systém má pouze jedno řešení
je-li hlavní determinant
. Li
a
= 0,= 0,= 0, pak má systém nekonečný počet řešení, která nelze najít pomocí Cramerových vzorců. Li
a
0, popř 0, popř 0, pak je soustava rovnic nekonzistentní, to znamená, že nemá řešení.

Příklad

Řešení:

1) Sestavme a vypočítejme hlavní determinant soustavy, skládající se z koeficientů neznámých.

.

Proto má systém unikátní řešení.

2) Složíme a vypočítáme pomocné determinanty, přičemž odpovídající sloupec v  nahradíme sloupcem volných členů.

Pomocí Cramerových vzorců najdeme neznámé:

,
,
.

Zkontrolujeme, zda je řešení správné

Tito.
.

, tj.

, tj.

Odpovědět: .

Příklad

Vyřešte soustavu rovnic Cramerovou metodou:

Řešení:

1) Složme a vypočtěme hlavní determinant systému z koeficientů neznámých:

.

V důsledku toho systém nemá jediné řešení.

2) Složíme a vypočítáme pomocné determinanty, přičemž odpovídající sloupec v  nahradíme sloupcem volných členů:

,
proto je systém nekonzistentní.

Odpovědět: systém je nekonzistentní.

Gaussova metoda

Gaussova metoda se skládá ze dvou fází. První fáze spočívá v postupném odstraňování proměnných z rovnic systému pomocí akcí, které nenarušují ekvivalenci systému. Uvažujme například první dvě rovnice soustavy (1).

(1)

Sečtením těchto dvou rovnic je nutné získat rovnici, ve které proměnná chybí ... Vynásobte první rovnici číslem a druhý na (
) a přidejte výsledné rovnice

Nahraďte koeficient před y, z a bezplatný člen na ,a respektive dostaneme novou dvojici rovnic

Všimněte si, že druhá rovnice neobsahuje proměnnou X.

Provedením podobných operací na první a třetí rovnici soustavy (1) a poté na druhé a třetí rovnici získané sčítáním transformujeme soustavu (1) do tvaru

(2)

Takový výsledek je možný, pokud má systém jedinečné řešení. V tomto případě se řešení nalézá pomocí obráceného průběhu Gaussovy metody (druhý stupeň). Z poslední rovnice soustavy (2) najdeme neznámou proměnnou z, pak z druhé rovnice zjistíme y, a X respektive z prvního, dosazením již nalezených neznámých do nich.

Někdy v důsledku sečtení dvou rovnic může mít celková rovnice jednu z následujících forem:

A)
, kde
... To znamená, že řešený systém je nekonzistentní.

B), tzn
... Taková rovnice je ze systému vyloučena, v důsledku toho je počet rovnic v systému menší než počet proměnných a systém má nekonečné množství řešení, jejichž nalezení ukáže příklad.

Příklad

Řešení:

Zvažte následující způsob implementace první fáze řešení Gaussovou metodou. Zapišme tři řady koeficientů pro neznámé a volné členy odpovídající třem rovnicím soustavy. Volné členy oddělte od koeficientů svislou čárou a pod třetí čárou nakreslete vodorovnou čáru.

Zakroužkujme první řádek, který odpovídá první rovnici soustavy – koeficienty v této rovnici zůstanou nezměněny. Místo druhého řádku (rovnice) je třeba získat řádek (rovnici), kde je koeficient at je nula. K tomu vynásobíme všechna čísla v prvním řádku (–2) a sečteme je s odpovídajícími čísly na druhém řádku. Výsledné součty zapisujeme pod vodorovnou čáru (čtvrtý řádek). Aby se místo třetího řádku (rovnice) dostal také řádek (rovnice), ve kterém je koeficient at je nula, vynásobte všechna čísla v prvním řádku (–5) a sečtěte je s odpovídajícími čísly ve třetím řádku. Výsledné součty zapíšeme do pátého řádku a pod něj nakreslíme novou vodorovnou čáru. Zakroužkujme čtvrtý řádek (nebo pátý dle výběru). Je vybrán řádek s nižšími koeficienty. V tomto řádku zůstanou koeficienty nezměněny. Místo pátého řádku musíte získat řádek, kde jsou dva koeficienty již rovny nule. Čtvrtou řadu vynásobíme 3 a přičteme k pátému. Částku napíšeme pod vodorovnou čáru (šestý řádek) a zakroužkujeme.

Všechny popsané akce jsou znázorněny v tabulce 1 pomocí aritmetických znamének a šipek. Řádky zakroužkované v tabulce zapíšeme opět ve formě rovnic (3) a použitím zpětného pohybu Gaussovy metody najdeme hodnoty proměnných X, y a z.

stůl 1

Obnovujeme systém rovnic získaný v důsledku našich transformací:

(3)

Obraťte Gaussovu metodu

Ze třetí rovnice
nalézt
.

Ve druhé rovnici soustavy
nahradit nalezenou hodnotu
, dostaneme
nebo
.

Z první rovnice
dosazením již nalezených hodnot proměnných získáme
, to je
.

Abyste se ujistili, že řešení je správné, je třeba provést kontrolu ve všech třech rovnicích soustavy.

Zkouška:

, dostaneme

Dostaneme

Dostaneme

pak je systém vyřešen správně.

Odpovědět:
,
,
.

Příklad

Vyřešte soustavu pomocí Gaussovy metody:

Řešení:

Postup v tomto příkladu je stejný jako v předchozím příkladu a konkrétní akce jsou uvedeny v tabulce 2.

V důsledku transformací získáme rovnici tvaru, proto je daný systém nekompatibilní.

Odpovědět: systém je nekonzistentní.

Příklad

Vyřešte soustavu pomocí Gaussovy metody:

Řešení:

Tabulka 3

V důsledku transformací získáme rovnici tvaru, který je vyloučen z uvažování. Máme tedy soustavu rovnic, ve které je počet neznámých 3 a počet rovnic 2.

Systém má nespočet řešení. Abychom našli tato řešení, zavedeme jednu volnou proměnnou. (Počet volných proměnných je vždy roven rozdílu mezi počtem neznámých a počtem rovnic zbývajících po transformaci soustavy. V našem případě 3 - 2 = 1).

Nech být
Je volná proměnná.

Pak z druhé rovnice najdeme
, kde
a pak najít X z první rovnice
nebo
.

Tím pádem,
;
;
.

Zkontrolujme rovnice, které se na hledání nepodílely a , tedy ve druhé a třetí rovnici původní soustavy.

Zkouška:

nebo, dostaneme
.

nebo, dostaneme
.

Systém byl vyřešen správně. Dát libovolnou konstantu jiné hodnoty, dostaneme jiné hodnoty X, y a z.

Odpovědět:
;
;
.

Cramerova metoda neboli tzv. Cramerovo pravidlo je způsob, jak hledat neznámé veličiny ze soustav rovnic. Lze ji použít pouze v případě, že počet hledaných hodnot je ekvivalentní počtu algebraických rovnic v systému, to znamená, že hlavní matice vytvořená ze systému musí být čtvercová a nesmí obsahovat nulové čáry, a také pokud její determinant musí nebýt nula.

Věta 1

Cramerův teorém Pokud se hlavní determinant $ D $ hlavní matice na základě koeficientů rovnic nerovná nule, pak je soustava rovnic konzistentní a má jedinečné řešení. Řešení takové soustavy se vypočítává pomocí tzv. Cramerových vzorců pro řešení soustav lineárních rovnic: $ x_i = \ frac (D_i) (D) $

Co je Cramerova metoda

Podstata Cramerovy metody je následující:

1. Abychom našli řešení systému Cramerovou metodou, nejprve vypočteme hlavní determinant matice $ D $. Když se vypočítaný determinant hlavní matice při výpočtu Cramerovou metodou ukázal jako nula, pak systém nemá jediné řešení nebo má nekonečný počet řešení. V tomto případě se pro nalezení obecné nebo nějaké základní odpovědi pro systém doporučuje použít Gaussovu metodu.
2. Poté je třeba nahradit extrémní sloupec hlavní matice sloupcem volných členů a vypočítat determinant $ D_1 $.
3. Opakujte totéž pro všechny sloupce a získáte determinanty od $ D_1 $ do $ D_n $, kde $ n $ je číslo sloupce zcela vpravo.
4. Po nalezení všech determinantů $ D_1 $ ... $ D_n $ můžete vypočítat neznámé proměnné podle vzorce $ x_i = \ frac (D_i) (D) $.

Techniky výpočtu determinantu matice

K výpočtu determinantu matice s rozměrem větším než 2 x 2 můžete použít několik metod:

• Pravidlo trojúhelníků neboli Sarrusovo pravidlo se podobá stejnému pravidlu. Podstata trojúhelníkové metody spočívá v tom, že při výpočtu determinantu součinu všech čísel spojených na obrázku červenou čárou vpravo se zapisují se znaménkem plus a všechna čísla jsou na obrázku spojena stejně na obrázku. vlevo - se znaménkem mínus. B obě pravidla jsou vhodná pro matice 3 x 3. V případě Sarrusova pravidla se nejprve přepíše samotná matice a vedle ní se znovu přepíše její první a druhý sloupec. Maticí se kreslí úhlopříčky a tyto další sloupce, členy matice ležící na hlavní diagonále nebo rovnoběžně s ní se píší se znaménkem plus a prvky ležící na vedlejší diagonále nebo rovnoběžně s ní se píší se znaménkem. znaménko mínus.

Obrázek 1. Pravidlo trojúhelníků pro výpočet determinantu pro Cramerovu metodu

• Pomocí techniky známé jako Gaussova metoda se tato technika také někdy označuje jako snižování řádu determinantu. V tomto případě je matice transformována a redukována na trojúhelníkový tvar a poté jsou vynásobena všechna čísla na hlavní diagonále. Je třeba si uvědomit, že při takovém hledání determinantu nemůžete násobit nebo dělit řádky nebo sloupce čísly, aniž byste je vyňali jako faktor nebo dělitel. V případě hledání determinantu je možné pouze odečítat a sčítat řetězce a pilíře dohromady s tím, že se předem vynásobí odečtený řetězec nenulovým faktorem. Také s každou permutací řádků nebo sloupců matice na místě byste měli pamatovat na nutnost změnit konečné znaménko matice.
• Při řešení SLAE se 4 neznámými Cramerovou metodou je nejlepší použít Gaussovu metodu k nalezení a nalezení determinantů nebo k určení determinantů pomocí hledání nezletilých.

Řešení soustav rovnic Cramerovou metodou

Aplikujeme Cramerovu metodu pro systém 2 rovnic a dvou požadovaných veličin:

$ \ začátek (případy) a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \ konec (případy) $

Pro větší pohodlí si jej ukážeme v rozšířené podobě:

$ A = \ begin (pole) (cc | c) a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \ end (pole) $

Pojďme najít determinant hlavní matice, nazývaný také hlavní determinant systému:

$ D = \ begin (pole) (| cc |) a_1 & a_2 \\ a_3 & a_4 \\ \ end (pole) = a_1 \ cdot a_4 - a_3 \ cdot a_2 $

Pokud hlavní determinant není nula, pak pro vyřešení slough Cramerovou metodou je nutné vypočítat několik dalších determinantů ze dvou matic s nahrazenými sloupci hlavní matice na řádek volných členů:

$ D_1 = \ začátek (pole) (| cc |) b_1 & a_2 \\ b_2 & a_4 \\ \ konec (pole) = b_1 \ cdot a_4 - b_2 \ cdot a_4 $

$ D_2 = \ začátek (pole) (| cc |) a_1 & b_1 \\ a_3 & b_2 \\ \ konec (pole) = a_1 \ cdot b_2 - a_3 \ cdot b_1 $

Nyní najdeme neznámé $ x_1 $ a $ x_2 $:

$ x_1 = \ frac (D_1) (D) $

$ x_2 = \ frac (D_2) (D) $

Příklad 1

Cramerova metoda pro řešení SLAE s hlavní maticí 3. řádu (3 x 3) a třemi požadovanými.

Řešte soustavu rovnic:

$ \ začátek (případů) 3x_1 - 2x_2 + 4x_3 = 21 \\ 3x_1 + 4x_2 + 2x_3 = 9 \\ 2x_1 - x_2 - x_3 = 10 \\ \ konec (případů) $

Vypočítejme hlavní determinant matice pomocí výše uvedeného pravidla pod položkou číslo 1:

$ D = \ begin (pole) (| ccc |) 3 & -2 & 4 \\ 3 & 4 & -2 \\ 2 & -1 & 1 \\ \ konec (pole) = 3 \ cdot 4 \ cdot ( -1) + 2 \ cdot (-2) \ cdot 2 + 4 \ cdot 3 \ cdot (-1) - 4 \ cdot 4 \ cdot 2 - 3 \ cdot (-2) \ cdot (-1) - (- 1) \ cdot 2 \ cdot 3 = - 12 - 8 -12 -32 - 6 + 6 = - 64 $

A nyní tři další determinanty:

$ D_1 = \ begin (pole) (| ccc |) 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \ konec (pole) = 21 \ cdot 4 \ cdot 1 + (- 2) \ cdot 2 \ cdot 10 + 9 \ cdot (-1) \ cdot 4 - 4 \ cdot 4 \ cdot 10 - 9 \ cdot (-2) \ cdot (-1) - (-1) \ cdot 2 \ cdot 21 = - 84 - 40 - 36 - 160 - 18 + 42 = - 296 $

$ D_2 = \ begin (pole) (| ccc |) 3 & 21 & 4 \\ 3 & 9 & 2 \\ 2 & 10 & 1 \\ \ konec (pole) = 3 \ cdot 9 \ cdot (- 1) + 3 \ cdot 10 \ cdot 4 + 21 \ cdot 2 \ cdot 2 - 4 \ cdot 9 \ cdot 2 - 21 \ cdot 3 \ cdot (-1) - 2 \ cdot 10 \ cdot 3 = - 27 + 120 + 84 - 72 + 63 - 60 = 108 $

$ D_3 = \ begin (pole) (| ccc |) 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \ konec (pole) = 3 \ cdot 4 \ cdot 10 + 3 \ cdot (-1) \ cdot 21 + (-2) \ cdot 9 \ cdot 2 - 21 \ cdot 4 \ cdot 2 - (-2) \ cdot 3 \ cdot 10 - (-1) \ cdot 9 \ cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = – 60 $

Najdeme požadované hodnoty:

$ x_1 = \ frac (D_1) (D) = \ frac (- 296) (- 64) = 4 \ frac (5) (8) $

$ x_2 = \ frac (D_1) (D) = \ frac (108) (-64) = - 1 \ frac (11) (16) $

$ x_3 = \ frac (D_1) (D) = \ frac (-60) (-64) = \ frac (15) (16) $

Cramerova metoda je založena na použití determinantů při řešení soustav lineárních rovnic. To značně urychluje proces řešení.

Cramerovu metodu lze použít k řešení soustavy tolika lineárních rovnic, kolik je v každé rovnici neznámých. Pokud determinant soustavy není roven nule, pak lze v řešení použít Cramerovu metodu, pokud je roven nule, pak nikoliv. Cramerovu metodu lze navíc použít k řešení soustav lineárních rovnic, které mají jedinečné řešení.

Definice... Determinant složený z koeficientů neznámých se nazývá systémový determinant a značí se (delta).

Determinanty

se získají nahrazením koeficientů odpovídajícími neznámými volnými členy:

;

.

Cramerův teorém. Pokud je determinant soustavy nenulový, pak soustava lineárních rovnic má jedno jedinečné řešení a neznámá je rovna poměru determinantů. Jmenovatel je determinant systému a čitatel je determinant získaný z determinantu systému nahrazením koeficientů v této neznámé volnými členy. Tato věta platí pro soustavu lineárních rovnic libovolného řádu.

Příklad 1.Řešte soustavu lineárních rovnic:

Podle Cramerův teorém my máme:

Takže řešení systému (2):

online kalkulačka, metoda Cramerova řešitele.

Tři případy při řešení soustav lineárních rovnic

Jak je zřejmé z Cramerovy věty, při řešení soustavy lineárních rovnic mohou nastat tři případy:

První případ: soustava lineárních rovnic má jedinečné řešení

(systém je konzistentní a jednoznačný)

Druhý případ: soustava lineárních rovnic má nekonečný počet řešení

(systém je konzistentní a neurčitý)

** ,

těch. koeficienty neznámých a volných členů jsou úměrné.

Třetí případ: soustava lineárních rovnic nemá řešení

(systém nekonzistentní)

Takže systém m lineární rovnice s n se nazývají proměnné nekonzistentní pokud nemá řešení, a kloub pokud má alespoň jedno řešení. Společná soustava rovnic, která má pouze jedno řešení, se nazývá určité a více než jeden - nedefinováno.

Příklady řešení soustav lineárních rovnic Cramerovou metodou

Nechť je daný systém

.

Na základě Cramerovy věty

………….
,

kde
-

systémový determinant. Zbývající determinanty získáme nahrazením sloupce koeficienty odpovídající proměnné (neznámé) volnými členy:

Příklad 2

.

Proto je systém definitivní. Abychom našli jeho řešení, vypočítáme determinanty

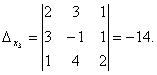
Podle Cramerových vzorců zjistíme:

Takže (1; 0; -1) je jediné řešení systému.

Chcete-li zkontrolovat řešení soustav rovnic 3 X 3 a 4 X 4, můžete použít online kalkulačku, která řeší Cramerovu metodu.

Pokud v soustavě lineárních rovnic v jedné nebo více rovnicích nejsou žádné proměnné, pak v determinantu jsou odpovídající prvky rovny nule! Toto je další příklad.

Příklad 3 Vyřešte soustavu lineárních rovnic Cramerovou metodou:

.

Řešení. Najdeme determinant systému:

Pozorně si prohlédněte soustavu rovnic a determinant soustavy a zopakujte odpověď na otázku, ve kterých případech se jeden nebo více prvků determinantu rovná nule. Takže determinant není roven nule, proto je systém určitý. Abychom našli jeho řešení, vypočítáme determinanty pro neznámé

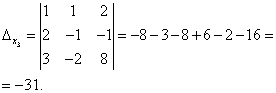
Podle Cramerových vzorců zjistíme:

Řešením systému je tedy (2; -1; 1).

Chcete-li zkontrolovat řešení soustav rovnic 3 X 3 a 4 X 4, můžete použít online kalkulačku, která řeší Cramerovu metodu.

Zpět na začátek stránky

Pokračujeme v řešení systémů Cramerovou metodou společně

Jak již bylo zmíněno, pokud je determinant systému roven nule a determinanty pro neznámé nejsou rovny nule, systém je nekonzistentní, to znamená, že nemá řešení. Ukažme si to na následujícím příkladu.

Příklad 6. Vyřešte soustavu lineárních rovnic Cramerovou metodou:

Řešení. Najdeme determinant systému:

Determinant systému je roven nule, proto je systém lineárních rovnic buď nekonzistentní a určitý, nebo nekonzistentní, to znamená, že nemá řešení. Pro upřesnění vypočítáme determinanty pro neznámé

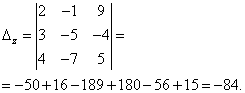
Determinanty pro neznámé se nerovnají nule, proto je systém nekonzistentní, to znamená, že nemá řešení.

Chcete-li zkontrolovat řešení soustav rovnic 3 X 3 a 4 X 4, můžete použít online kalkulačku, která řeší Cramerovu metodu.

V úlohách o soustavách lineárních rovnic jsou i takové, kde jsou kromě písmen označujících proměnné i další písmena. Tato písmena představují určité číslo, nejčastěji reálné číslo. V praxi jsou takové rovnice a soustavy rovnic vedeny problémy hledání obecných vlastností libovolných jevů a objektů. To znamená, že jste vynalezli nějaký nový materiál nebo zařízení a k popisu jeho vlastností, které jsou běžné bez ohledu na velikost nebo počet vzorku, potřebujete vyřešit soustavu lineárních rovnic, kde místo nějakých koeficientů proměnných jsou písmena. Pro příklady nemusíte chodit daleko.

Další příklad je pro podobnou úlohu, jen se zvyšuje počet rovnic, proměnných a písmen označujících nějaké reálné číslo.

Příklad 8. Vyřešte soustavu lineárních rovnic Cramerovou metodou:

Řešení. Najdeme determinant systému:

Najděte determinanty pro neznámé